News & Events
[알고리즘 트레이딩/시장미시구조] 43. 주문 집행 알고리즘 (4) – VWAP 집행 알고리즘 (1)
시장미시구조론 (Market Microstructure) – (43)
주문 집행 알고리즘 (4) – VWAP 집행 알고리즘 (1)
이전 시간에는 총 거래비용 (Implementation shortfall)의 효용이 최소가 되는 최적 집행 알고리즘에 대해 살펴보았다. 이번에는 VWAP을 평가가격 (Benchmark Price)으로 설정 했을 때 집행 결과인 vwap 이 시장 VWAP 에 가까워지도록 집행하는 알고리즘에 대해 살펴본다.
VWAP (Volume Weighted Average Price)은 거래량 가중평균 가격을 의미하며, 아래 식으로 산출할 수 있다.
최적 VWAP 집행 알고리즘이란, vwap = VWAP 이 되도록 하는 것이다. 물론, 매수할 때는 싸게 매수하고, 매도할 때는 비싸게 매도하는 알고리즘이 좋겠지만, 어느 선까지 싸게 매수 (비싸게 매도)할 것인지 기준이 필요하다. 집행 시작 시점에서는 종료 시점의 주가나 거래량을 미리 알 수 없으므로, 시장보다 싸게 매수하거나, 비싸게 매도할 방법은 없다. VWAP을 평가가격으로 설정했다는 의미는, 종료 시점에서 평가했을 때 시장 평균 가격 정도에 목표 수량을 집행했다면 성공적이라는 것을 의미한다. 즉, vwap = VWAP 이면 100점짜리 알고리즘이라는 의미이다.
vwap = VWAP 의 목표를 달성하려면 시장에서 발생하는 거래량에 비례해서 집행할 필요가 있다. 만약, 금일 09:00:00 ~ 15:00:00 사이에 삼성전자 주식 5,000 주를 분할 매수할 계획이라면 09:00 ~ 09:30 사이에는 몇 주를 집행하고, 9:30 ~ 10:00 사이에는 몇 주를 집행할 것인지, 해당 시간에 발생할 거래량을 예측하여 결정한다. 그러나 금일 발생할 거래량을 예측하는 것은 대단히 어려운 일이다. 금일 발생할 거래량은 과거 데이터를 참조하여 추정할 수밖에 없다.
아래 그림은 삼성전자의 최근 5일간 발생한 거래량이다 (2월 29일은 제외하였음). 대체적으로 장 개장 직후에 거래량이 많고, 장 중반에는 거래량이 작다가, 장 종료 직전에 거래량이 높다. 목표 달성을 위해서는 이 패턴을 참조하여 집행하는 것이 좋을 것이다.
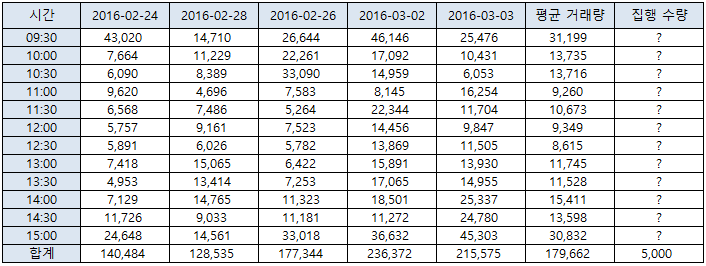
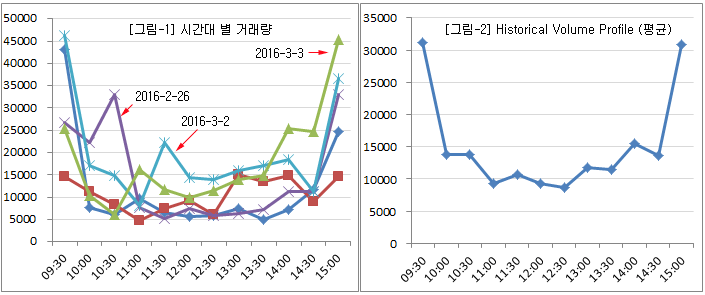
아래 그림은 위의 데이터를 그래프로 그려본 것이다. [그림-1] 시간대 별 거래량을 보면 대체적으로 U-자형에 가까운 패턴을 보인다. [그림-2] 는 5일간의 평균 거래량이다. 금일 삼성전자에 큰 이슈가 없다면 이 패턴대로 집행하는 것도 한 방법이 될 수 있다.
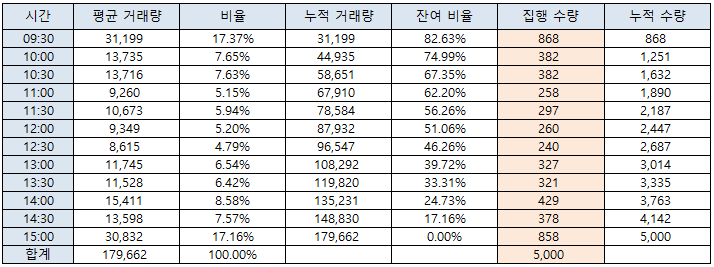
아래 그림은 최근 5일간 발생한 거래량 비율대로 집행 수량을 결정해 본 것이다. 금일 삼성전자 주식 5,000 주를 매수할 계획이라면, 09:00 ~ 09:30 사이에는 868 주를 매수하고, 09:30 ~ 10:00 사이에는 382 주를 매수한다. 여기서는, 설명을 간단히 하기위해 30분 단위를 사용하였지만, 10분 단위, 5분 단위, 1분 단위 등으로 구간을 짧게 설정할 수 있다.
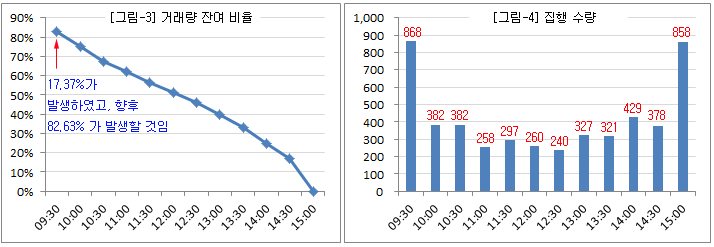
아래 그림은 위의 데이터를 그림으로 그린 것이다. [그림-4] 집행 수량의 패턴은 최근 5일간 발생한 평균 거래량 패턴과 동일하다. 금일 삼성전자에 큰 호재나, 악재가 없다면 금일 거래량도 최근 5일간 평균 패턴과 유사할 것으로 가정하고 집행 계획을 수립한 것이다. [그림-3] 거래량 잔여 비율은 해당 시간에 앞으로 발생할 거래량이 전체 거래량 대비 몇 퍼센트 남았는지를 확인해 본 것이다. 집행을 위해서는 이미 발생한 거래량보다, 앞으로 발생할 거래량에 더 관심이 있으므로 잔여 비율 척도를 사용하는 것도 좋다 (다음 시간에 살펴볼 최적화 이론에서 잔여 비율 척도를 사용하므로, 여기서 미리 확인해 본 것임.)
이 결과는 단순히 최근 거래량을 참조하여 단순 비율로 집행 수량을 추정해 본 것으로, 최적 집행 수량을 결정했다고 보기는 어렵다. 최적 알고리즘을 찾는 방법은 수없이 많을 것이고, 지금도 연구되고 있다. 한 예로 아래와 같이 목표를 설정하여 집행 수량을 결정해 볼 수도 있다.
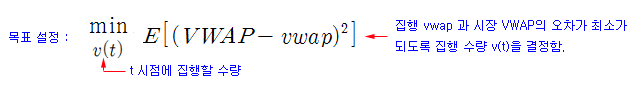
위의 목표 함수는 t-시점에 집행할 수량 v(t)를 control 변수로 하여 (VWAP – vwap)의 오차가 최소가 되는 v(t)의 조건을 찾는 문제이다. 이 문제에 대해서는 다음 시간에 자세히 살펴보기로 한다.
