News & Events
[알고리즘 트레이딩/시장미시구조] 44. 주문 집행 알고리즘 (5) – Konishi의 최적 VWAP 집행 알고리즘
시장미시구조론 (Market Microstructure) – (44)
주문 집행 알고리즘 (5) – Konishi의 최적 VWAP 집행 알고리즘
이전 시간에는 시장에서 발생한 과거 거래량 (Historical Volume Profile)을 참조하여 단순 비율로 vwap 집행 계획을 수립해 보았다. 이번 시간에는 아래 목표와 같이 시장 VWAP과 집행 vwap의 오차가 최소가 되도록 집행 계획을 수립해 본다.
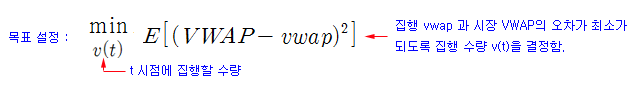
2002년 Hizuru Konishi는 “Optimal slice of a VWAP trade” 라는 논문에서 위의 최적화 문제를 다루었다. Konishi는 위의 목표를 계산하기 위해 vwap과 VWAP을 아래와 같이 연속 모형으로 정의하였다. 주문 집행자가 시장에 참여하면 시장 거래량은 집행 물량만큼 늘어날 것이므로 시장 VWAP을 식 2)와 같이 정의하였다.
아주 작은 물량으로 연속적으로 주문을 집행하면 시장 충격은 작을 것으로 간주하여, 시장 충격은 없는 것으로 가정하였다. vwap과 VWAP의 오차 (오차의 제곱)는 식 3)으로 나타낼 수 있고, 거래량이나 집행 물량 척도 대신 잔여 거래량과 잔여 집행량 비율을 최적화를 위한 척도로 사용하였다. 잔여 거래량 비율 (Xt)은 총 거래량 대비 t 시점 이후로 발생할 거래량의 비율이고, 잔여 집행량 비율 (xt)은 총 집행 물량 대비 t 시점 이후로 집행할 물량의 비율이다.
식 3)의 과정은 Konishi 논문의 Appendix A에 상세히 나와 있다. 식 3)에서 집행 물량이 시장 거래량보다 매우 작다면 공분산 항은 식 0 으로 간주할 수 있으므로, 식 3)은 식 5)로 간단히 표현할 수 있다.
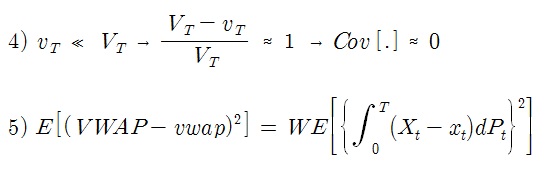
주가 (Pt)가 브라운운동 (Bt)을 따르는 것으로 간주하면 식 6)으로 표현할 수 있다. 식 6)의 주가 모형은 집행 기간 동안의 단기간 주가이므로 Drift = 0 이고, 변동성의 단위는 주가이다 (수익률이 아님). 식 6)을 이용하면 식 5)를 식 7)로 표현할 수 있다. (dBt dBt = dt 임, stochastic calculus).
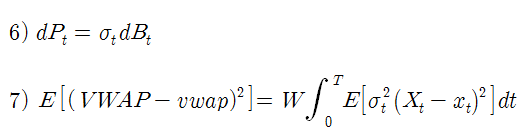
우리의 목표는 식 8)을 최소화 시키는 xt 의 조건을 찾는 것이다. 식 8)을 전개한 후 완전제곱식의 형태로 나타내면 식 10) 이 된다. 식 10)의 첫 번째 항은 xt 와 무관하므로, 두 번째 항이 최소가 되는 조건을 찾으면 된다.
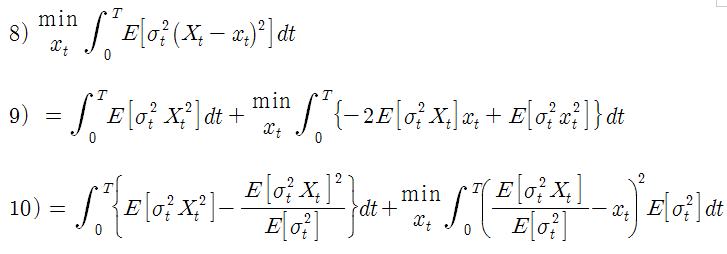
식 10) 의 두 번째 항이 최소가 되려면 괄호의 제곱 항이 0 이 되어야 하므로, 최적 xt 는 식 11) 이 되고, 식 11)을 풀어 쓰면 식 12) 가 된다. 여기서 xt 는 t ~ T 기간 동안 집행해야할 집행량의 비율이며, t-시점의 집행 수량 대신 잔여 집행 비율을 최적화한 것이다. 식 12)를 보면 잔여 집행 비율은 잔여 시장 거래량 비율의 기대치와 (E[Xt]) 밀접한 관계가 있다는 것을 알 수 있다. 만약, 공분산 항이 0 이라면 집행 잔여 비율은 시장 잔여 비율의 기대치와 완전히 일치한다. 공분산 항이 양수일지, 음수일지, 0 일지는 직관적으로 이해하기가 쉽지 않다. t-시점의 변동성이 높을 때 시장 거래량이 증가하는 것은 맞지만 (양의 상관관계), 잔여 시장 거래량 비율도 높아지는지에 대해서는 별도의 논의가 필요할 것 같다.
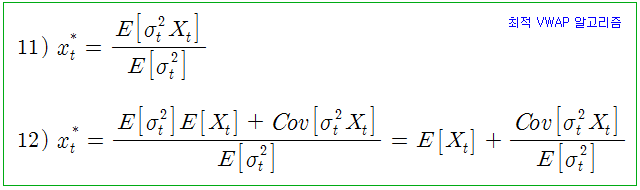
여기까지 Konishi 논문의 기본 아이디어에 대해 살펴보았다. 논문에는 최적 집행 시점 알고리즘, Multiple stock 에 대한 최적 알고리즘 등 유용한 정보가 더 많이 있으나, 본 블로그에서는 여기까지만 살펴보기로 한다. 다음 시간에는 식 12)를 이용하여, 이전 시간에 살펴본 삼성전자의 집행 계획을 수정해 보기로 한다.
Reference :
[1] Hizuru Konishi, 2002, Optimal slice of a VWAP trade
