[알고리즘 트레이딩/시장미시구조] 7. 시장가 주문의 연속성

시장미시구조론 (Market Microstructure) – (7)

시장가 주문의 연속성

여러 투자자들을 대하다보면 당장 돈이 되는 전략을 찾아내려는 성급함을 종종 보게 된다. 투자의 목적이 수익의 창출이기 때문에 당연히 이해는 간다. 그러나 시장의 내면을 충분히 이해하지 못한 상태에서 만든 전략은 일시적일 수밖에 없고, 시장의 변화에 약할 수밖에 없다. 시장의 특성이 충분히 반영되고, 시장의 변화에 잘 적응할 수 있어야 강한 전략이라 할 수 있을 것이다.

이러한 맥락에서, 이번 시간에는 시장가 주문의 연속성에 대한 특성을 살펴보기로 한다. 틱 데이터 중 체결데이터에는 시장가 주문의 체결량과 체결가격이 포함되어 있다. 이 데이터를 이용하여 시장가 주문의 흐름을 살펴보면 주문의 연속성이 존재함을 알 수 있다. 즉, 시장가 매수 주문 뒤에 매수 주문이 따라 나오거나, 매도 주문 뒤에 매도 주문이 이어지는 경향을 볼 수 있다. 이 현상은 추세를 추종하려는 움직임 때문이기도 하고, 많은 양의 거래를 원하는 주체 (Informed trader)의 분할 주문 때문이기도 하다.

아래 그림은 특정일의 코스피200 지수 선물의 체결데이터를 분석한 것이다 (09:00 ~ 09:34 까지 10,000개의 틱 데이터). 4번째 열에 시장가 주문 수량이 기록되어 있고 (+ : 매수 수량, – : 매도 수량), 5번째 열 (시장가 Indicator)에는 수량과 상관없이 매수, 매도 상황만을 표시하였다. +1 이면 시장가 매수 주문이 발생한 것이고, -1 이면 매도 주문이 발생한 것이다.

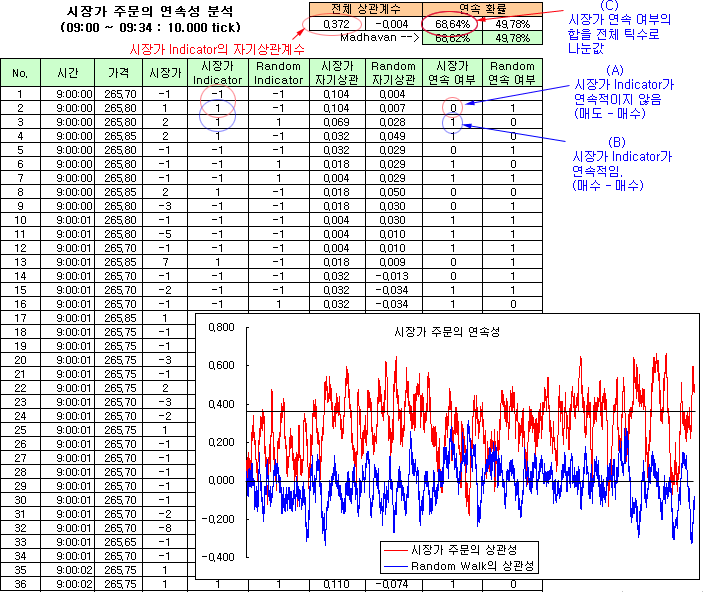
9번째 열 (시장가 연속 여부)에는 주문이 연속적인지 아닌지를 표시하였다. 첫 번째는 시장가 Indicator가 -1 뒤에 +1이 나왔으므로, 시장가 연속 여부는 0으로 표시하였다. 두 번째는 시장가 Indicator가 +1 뒤에 또 +1이 나왔으므로, 시장가 연속 여부는 1로 표시하였다. 전체 10,000개 틱 데이터 중에 시장가 연속 여부가 1인 개수를 세어보면 연속 확률을 계산해 볼 수 있다. 위의 그림은 10,000개 틱 중에 6,864개가 연속적이므로, 연속 확률이 약 68.64% 로 계산되었다. 이 의미는 시장가 매수 주문 뒤에 또 매수 주문이 유입될 확률이 약 68.64%라는 의미이다 (매도 주문도 마찬가지임).

위의 경우와 비교해 보기위해 Random으로 Indicator를 생성하여 동일한 과정을 거치면 연속확률이 약 49.78%가 나온다. 즉, Random의 경우는 매수 주문 뒤에 또 매수 주문이 나올 확률이 약 50%라는 의미로 연속성이 존재하지 않는다는 것을 알 수 있다.

시장가 주문 Indicator의 자기상관계수 (시차=1)를 계산해 보면, 위의 그림과 같이 0.372가 나온다. 보통 자기상관계수가 0.2보다 크면 자기상관성이 존재한다고 볼 수 있으므로, 위의 시장가 주문 Indicator는 자기상관성이 존재한다고 할 수 있다.

시장가 주문 Indicator는 정상성을 갖는 시계열이므로 (Stationary), AR(1) 모형을 적용해 볼 수 있다. 아래 그림은 시장가 주문 Indicator를 AR(1)에 적용했을 때 연속 확률을 계산해 본 것이다. t=0 시점에 매수 주문 (+1)이 발생했을 때, t=1 시점에는 매수 주문 (+1)이 발생할 수도 있고, 매도 주문 (-1)이 발생할 수도 있다. AR(1) 모형을 이용하면 t=1 시점에 발생할 주문의 확률 (p)을 계산해 볼 수 있다. (페어트레이딩 – AR(1) 모형 참조)

매수 주문 뒤에 매수 주문이 이어질 확률을 p 라 하고, t=1 시점의 기댓값을 계산해 보면, 위 그림에 있는 수식의 좌변과 같이 쓸 수 있다. 또한, AR(1) 모형에서 다음 기의 기댓값은 제1단계 전방예측값이 되고, 1단계 전방예측값은 자기상관계수 (시차=1)가 된다. 따라서 다음 기의 기댓값은 자기상관계수가 된다. 이 논리를 이용하면 연속 확률 p를 위와 같이 표현할 수 있다. 자기상관계수가 0 인 경우는 연속성이 존재하지 않는 경우이므로 연속 확률이 50%가 나온다.

이 수식을 이용하여 맨 위 그림의 연속 확률을 계산해 보면 68.62%가 나온다. 실측 결과인 68.64%와 거의 일치한다. 따라서 시장가 주문 Indicator를 AR(1) 모형에 적용하는 것은 무리가 없어 보이고, 실시간으로 자기상관계수를 구하면, 실시간으로 시장가 주문의 연속성을 파악하여 전략에 이용해 볼 수 있다. 또한 AR(1)의 특성을 이용하면, 연속 확률 이외의 다른 특성들도 파악해 볼 수 있다 (다음 시간에…).

이번에는 위의 논리를 일반적인 거시 시장 (Macro market)에 적용해 보자. 아래 그림은 종합주가 지수와 투자자별 순 매수 현황을 집계한 것이다 (HTS에서 수집). 투자자별 순 매수 현황을 Indicator로 표현하여 (매수 혹은 매도), 위의 논리대로 연속 확률을 계산해 보았다.

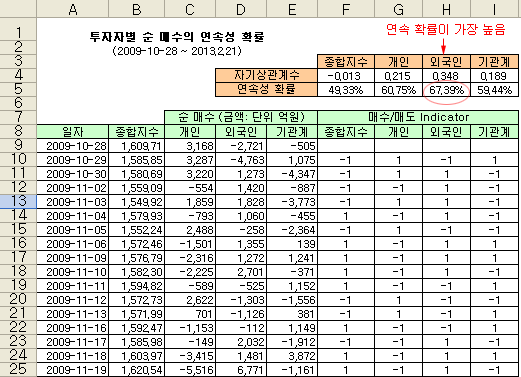
종합지수의 경우는 연속 확률이 49.33%로 연속성이 없음을 알 수 있다. 즉, 오늘 종합주가 지수가 올랐어도, 내일 또 오를 확률은 거의 50%이다. 개인 투자자와 기관계는 약 60%로 약간의 연속성 있는 것으로 보이나, 자기상관계수가 약 0.2로 연속성이 있다고 단정하기는 어렵다. 그러나 외국인 투자자의 경우는 자기상관계수가 0.348로 자기상관성이 (작지만) 존재하고, 매수의 연속 확률도 67.39%로 가장 높게 계산되었다. 즉, 외국인 투자자는 꾸준히 매수하거나, 꾸준히 매도하는 경향이 가장 높은 것을 알 수 있다 (실측 확률도 유사하게 계산되었음).

이번 시간에는 시장 데이터 관측을 통한 주문의 연속성에 대해 알아보았다. 다음 시간에는 이 특성과 관련된 이론적인 모형을 다루어 보고, 좀 더 의미 있는 시장의 특성을 도출해 보기로 한다.

[출처]7. 시장가 주문의 연속성|작성자아마퀀트