News & Events
[Machine Learning] 26. 머신러닝에서 문제를 해결하는 방안
- 2019년 1월 14일
- Posted by: 인사이트캠퍼스
- Category: 금융/AI/IT 기사

바로 이전 내용에서 처음 슬라이드로 다시 돌아가서,
아래 그림과 같이 머신 러닝을 적용할 때 문제가 발생하면 조치를 할 수 있는 옵션들이 약 6가지 정도 있습니다.
그냥 감으로 이것저것 해보는 것은 시간이 오래걸리기 때문에 효율적으로 판단하는 방법을 이전 내용에서 배웠습니다. 이제 이것을 통해서 어떠한 조치를 취하는 것이 현재 내가 격고 있는 어려움에 효과적인지를 정리하면서 알아보겠습니다.
앞의 방법들을 사용해서 진단한 결과가 어떠한가에 따라서 방안을 선택하시면 됩니다.
만약 현재 내가 격고 있는 문제가 High Variance라고 진단 결과가 나왔다면 다음과 같은 조치들이 효과적입니다.
– training 데이터를 더 많이 모는 것
– features set을 줄여 보는 것
– lambda 크기를 크게 변경해 보는 것
반대로, 현재 내가 격고 있는 문제가 High Bias라고 하면 다음과 같은 다른 조치들이 효과적입니다.
– features를 더 많이 추가 해보는 것
– polynomial features를 추가 해보는 것
– lambda 크기를 작게 변경해 보는 것

Neural Network 의 구성에서도 비슷하게 적용을 할 수 있습니다.
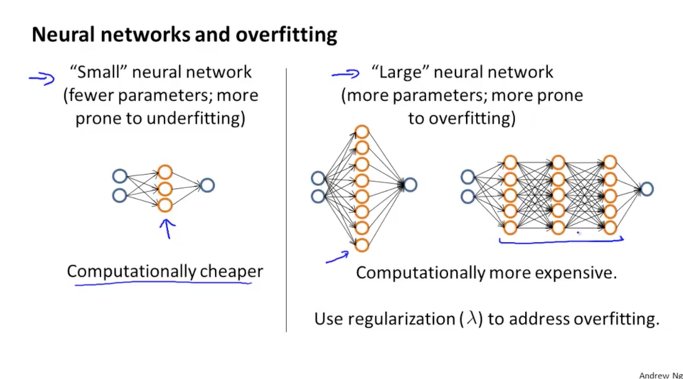
만약 작은 규모의 NN 구성이라면,
즉 features나 parameters가 적고 hidden layer가 최소 디폴트인 1개를 가지고 있는 경우에는 underfitting 의 경향을 보일 수 있고 대신 심플하기 때문에 연산에 들어가는 비용이 저렴합니다.
큰 규모의 NN 구성이라면,
features나 parameters가 많고 hidden layer가 다수개로 구성이 되어 있으므로 overfitting 의 가능성이 커지고 복잡한 구조와 연산을 하기 때문에 이에 대한 비용이 커집니다. 이런 경우에는 정규화식의 lambda를 사용해서 overfitting을 조절할 수 있습니다.
기본적으로는 hidden layer를 기본인 1개로 시작하면서 J cv로 error를 체크해보면서 hidden layer를 하나씩 늘려가보는 방법으로 구성을 하는 것이 좋습니다. 물론 이와 같이 NN 에서도 dataset 을 3가지(train, cv, test)로 분리 해서 사용하는 것이 좋습니다.
References
이외에 이러한 문제들을 해결하는 방안에 대한 정리된 내용이 있어 아래와 같이 추가합니다.
Model Selection:
Choosing M the order of polynomials.
How can we tell which parameters Θ to leave in the model (known as “model selection”)? There are several ways to solve this problem:
Get more data (very difficult).
Choose the model which best fits the data without overfitting (very difficult).
Reduce the opportunity for overfitting through regularization.
Bias: approximation error (Difference between expected value and optimal value)
High Bias = UnderFitting (BU)
Jtrain(Θ) and JCV(Θ) both will be high and Jtrain(Θ)≈JCV(Θ)
Variance: estimation error due to finite data
High Variance = OverFitting (VO)
Jtrain(Θ) is low and JCV(Θ)≫Jtrain(Θ)
Intuition for the bias-variance trade-off:
Complex model => sensitive to data => much affected by changes in X => high variance, low bias.
Simple model => more rigid => does not change as much with changes in X => low variance, high bias.
One of the most important goals in learning: finding a model that is just right in the bias-variance trade-off.
Regularization Effects:
Small values of λ allow model to become finely tuned to noise leading to large variance => overfitting.
Large values of λ pull weight parameters to zero leading to large bias => underfitting.
Model Complexity Effects:
Lower-order polynomials (low model complexity) have high bias and low variance. In this case, the model fits poorly consistently.
Higher-order polynomials (high model complexity) fit the training data extremely well and the test data extremely poorly. These have low bias on the training data, but very high variance.
In reality, we would want to choose a model somewhere in between, that can generalize well but also fits the data reasonably well.
A typical rule of thumb when running diagnostics is:
More training examples fixes high variance but not high bias.
Fewer features fixes high variance but not high bias.
Additional features fixes high bias but not high variance.
The addition of polynomial and interaction features fixes high bias but not high variance.
When using gradient descent, decreasing lambda can fix high bias and increasing lambda can fix high variance (lambda is the regularization parameter).
When using neural networks, small neural networks are more prone to under-fitting and big neural networks are prone to over-fitting. Cross-validation of network size is a way to choose alternatives.
References:
https://class.coursera.org/ml/lecture/index
http://www.cedar.buffalo.edu/~srihari/CSE555/Chap9.Part2.pdf
http://www.cedar.buffalo.edu/~srihari/CSE574/Chap3/Bias-Variance.pdf

