News & Events

* 이 글은 datadriveninvestor에 작성된 Sara Mohammed의 글을 번역하였습니다.

Subreddits, Quora Spaces와 수많은 블로그에 암호 화폐 시장에서 수익을 얻을 수 있는 방법들이 가득하지만 실은 말처럼 쉽지가 않다. “바이 더 딥(buy the dip)”과 같은 조언만으로는 도움이 되지 않는다. 다른 사람들보다 더 나은 성과를 내기 위해서 더 계산적이고 정보에 입각한 결정을 내리도록 할 수 있는 것들이 많다.
이를 위한 한 가지 방법은 긍정적인 방식으로 추세를 따라가고 추세가 역전되려 할 때 정신을 바짝 차리는 것이다. 수많은 지표와 패턴이 있지만, 모든 시장 상황에 적용할 수 있는 하나의 지표는 없다.
이것이 바로 트레이더들이 트렌드 시장이나 레인지 바운드 시장에서 도움이 되는 많은 지표들을 사용하는 이유이다. 그러나 트레이더가 이용할 수 있는 모든 종류의 지표를 사용한다는 것은 아니다. 사실 종종 너무 많은 지표를 사용하는 것은 부정적인 영향을 미칠 수 있고 더 많은 혼란을 일으킬 수 있다.
시간이 지남에 따라 트레이더들은 차트 리딩 능력을 강화하면서, 거래 스타일에 가장 적합한 지표로 지표의 수를 최소화한다. 이 포스팅에서는 이동 평균과 상대 강도 지수(relative strength index)에 대해 설명할 것이다. 우리는 지표를 효율적으로 사용하는 방법을 살펴보겠지만, 기술적인 부분에 대해서는 깊이 파고들지 않을 것이다. 이번 포스팅을 통해 기술 분석 기술을 향상 시킬 수 있을 것이다.
이동 평균
암호 거래에 일반적으로 사용되는 지표는 이동 평균이다. 이동 평균은 가격 이동이 이미 발생한 후 피드백을 제공하기 때문에 추세를 따른다. 이동 평균은 여러 가지 방법으로 계산할 수 있으며, 기간은 주요 매개 변수이다. 그 중 가장 널리 사용되는 것은 20, 50 및 200 주기 이동 평균이다. 단기 트레이더들도 5년, 10년 이동 평균선을 사용하지만 이는 모든 트레이더들에게 좋은 선택은 아닐 수 있다.
이동 평균에는 네 가지 유형(단순, 지수, 평활 및 가중)이 있지만, 가장 널리 사용되는 유형은 단순 및 지수 이동 평균이다. 계산을 위해 지수 이동 평균(EMA)은 최근 가격 데이터에 대한 가중치를 더 많이 제공한다. 따라서 가격 변화에 빠르게 반응한다. 반면, 단순 이동 평균은 가격 데이터와 동일한 가중치를 제공하기 때문에 가격 변화에 비교적 더디게 반응한다.
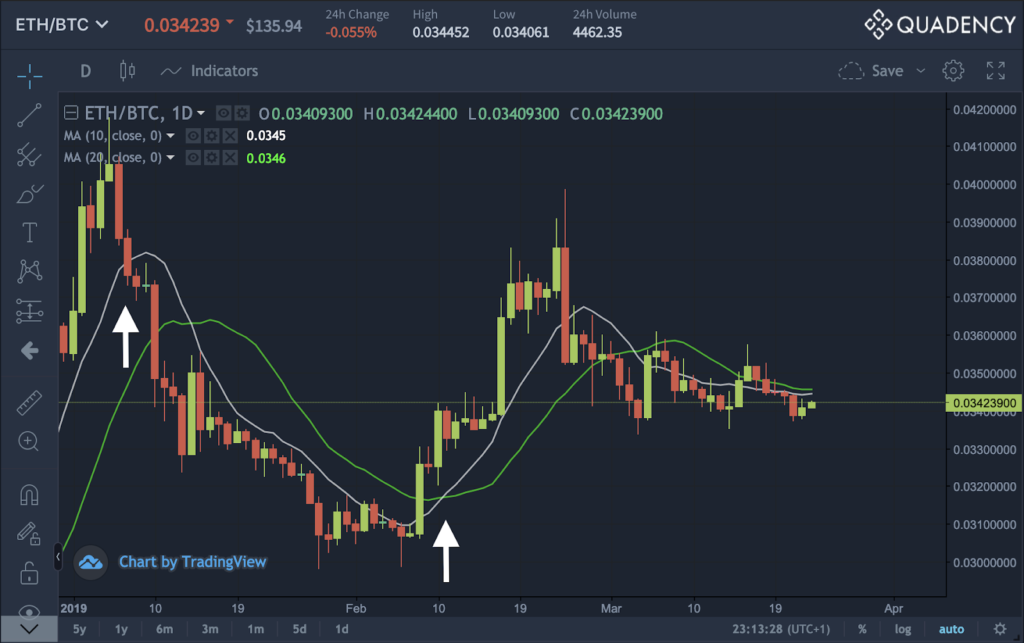
그래서 우리는 EMA를 더 짧은 기간 동안 사용하는 트레이더들을 보게 된다. 아래 예제에서 10일 이동 평균은 흰색, 20일 이동 평균은 녹색으로 나타난다. 이동 평균을 사용하는 두 가지 주요 방법은MA를 가로지르는 가격(예: 1월 3일) 또는 두 개의 MA에서 서로 다른 시간 간격(예: 2월 10일)을 찾는 것이다.
상대강도지수(RSI)
상대 강도 지수(RSI)는 진동자로, 경계 범위 내에서 움직인다. 가격 이동 속도와 변화에 대한 데이터를 담고 있으며 0에서 100 사이의 값을 가질 수 있다.
일반적으로 RSI 값에는 세 가지 주요 범위가 있다. 첫째, 30 미만의 값을 과매도(약세 시장에서는 과매도된 영역을 20개까지), 70개 이상의 값을 과매수(강세 시장에서는 과매수된 영역을 80개까지 이동할 수 있음)라고 한다. 세 번째로 고려해야 할 범위는 RSI가 긴 시간 동안 50 언저리를 교차할 때이다. 이는 RSI에 가장 널리 사용되는(즉, 발산을 발견하는 것) 중 하나인 잠재적 추세 반전을 나타낼 수 있다.
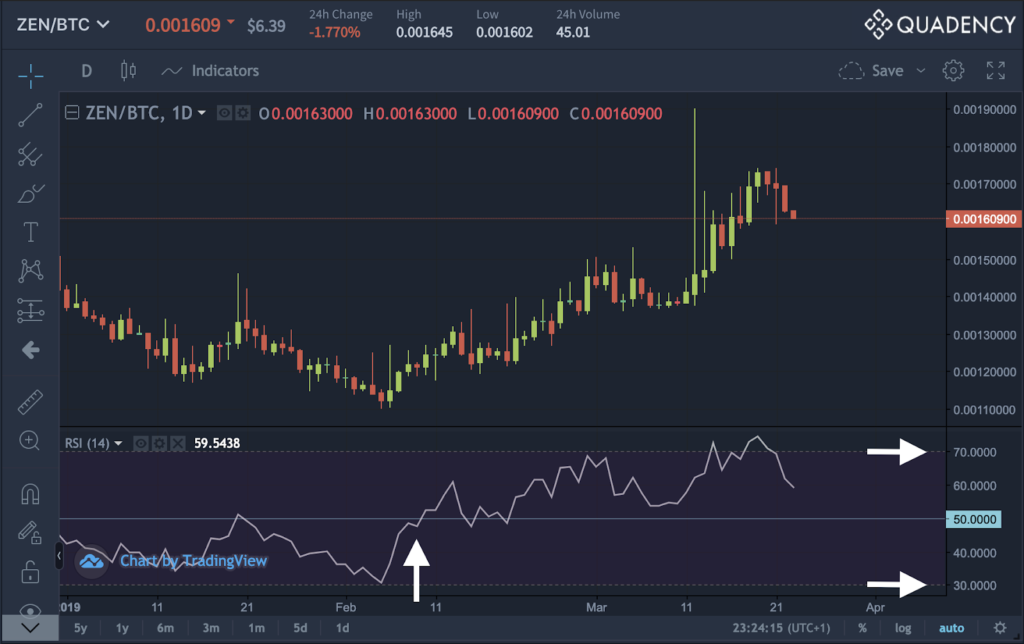
다음 이미지는 RSI가 2월 10일에 50 레벨을 교차한 후 추세 반전을 통해 이를 보여준다.
맺음말
많은 신규 투자자들에게 이동 평균과 RSI는 시장의 동향을 파악하기 위해 배우는 첫 번째 지표이다. 투자자들이 시장에 역행하고 불에 타는 것을 피할 수 있도록 하기 위함이다.
주의사항: 모든 투자는 위험을 수반한다. 결정을 내리기 전에, 특히 투자 기회에 관한 한 리서치를 스스로 해야한다.
8월 7일(토)에 개설되는
[실시간 온라인] 4대 공개형 블록체인 입문 2기
강의를 통해 블록체인에 관하여 심화 학습할 수 있습니다.
인사이트 캠퍼스에서 확인해보세요!
번역 – 핀인사이트 인턴연구원 강지윤(shety0427@gmail.com)
원문 보러가기>


