[알고리즘트레이딩/전략편] 10. 알고리즘 트레이딩 – 옵션의 페어트레이딩 (4)

알고리즘 트레이딩 (Algorithmic Trading) – 전략 (10)

알고리즘 트레이딩 – 옵션의 페어트레이딩 (4)

(델타헤지 전략 – Draft)

“이 전략은 본 블로그의 페어 트레이딩 기초편 (1~9)의 사전지식을 요합니다.”이전 3편의 포스트에서 소개한 옵션의 페어트레이딩은 매수/매도 계약수를 동일하게 적용한 경우였다. 이번에는 델타헤지를 통해 매도/매수 계약수를 다르게 적용하면 스프레드에 어떤 변화가 생기는지 살펴보자.

아래 그림은 필자가 만든 합성옵션계산기로 헤지 비율을 조정하여 그려본 합성 그래프이다. 아래의 왼쪽 그림은 행사가격이 277.5인 콜옵션을 매수하였을 때의 손익 그래프이고, 오른쪽 그림은 행사가격이 280.0인 콜옵션을 매도하였을 때의 손익 그래프이다.

알고리즘 트레이딩 – 옵션의 페어트레이딩 (4)

(델타헤지 전략 – Draft)

“이 전략은 본 블로그의 페어 트레이딩 기초편 (1~9)의 사전지식을 요합니다.”이전 3편의 포스트에서 소개한 옵션의 페어트레이딩은 매수/매도 계약수를 동일하게 적용한 경우였다. 이번에는 델타헤지를 통해 매도/매수 계약수를 다르게 적용하면 스프레드에 어떤 변화가 생기는지 살펴보자.

아래 그림은 필자가 만든 합성옵션계산기로 헤지 비율을 조정하여 그려본 합성 그래프이다. 아래의 왼쪽 그림은 행사가격이 277.5인 콜옵션을 매수하였을 때의 손익 그래프이고, 오른쪽 그림은 행사가격이 280.0인 콜옵션을 매도하였을 때의 손익 그래프이다.

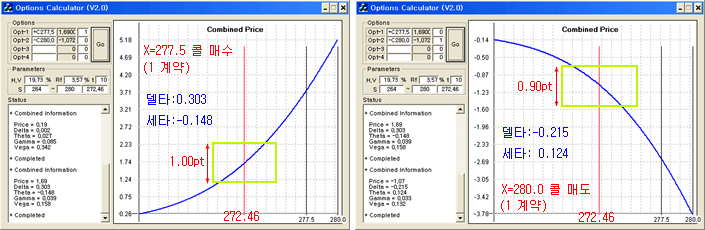
아래 왼쪽 그림은 이전 포스트에서 실험했던 매수/매도 1계약씩으로 페어 트레이딩을 했을 때의 손익 그래프이다. X=277.5 콜을 1계약 매수할 때, X=280.0을 1계약 매도하는 포지션이다. 손익이 기초자산의 증감에 따라 변하므로, 스프레드도 기초자산에 따라 변한다. 따라서 페어 트레이딩으로 적합하지 않은 모형이었다.오른쪽 그림은 이번 시간에 소개할 델타헤지를 적용한 페어 트레이딩의 손익구조이다. 델타헤지로 매수/매도 수량을 조절하면 합성 손익구조는 아래의 오른쪽 그래프와 같이 된다. 기초자산 가격의 주변에서 손익구조가 다른 것에 비해 완만하여 (초록색 박스) 스프레드도 완만하게 움직일 것으로 기대된다. 따라서 스프레드가 어느 정도 정상성을 가질 수 있고, 페어 트레이딩의 효과가 있을 것으로 기대된다. (주가가 상승할 때 그래프가 급격히 하락하는 것처럼 보이는데, y-축의 스케일이 작으므로 다른 그래프에 비해 더 심하게 하락하는 것은 아니다. 왼쪽 그래프와 동일한 스케일로 그리면 거의 평평한 수준이다.)

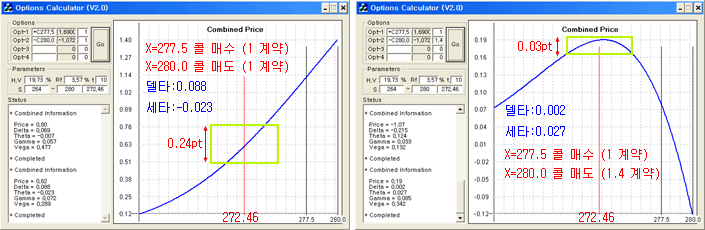
위의 오른쪽 그래프를 자세히 분석해 보자. 이 그래프는 알고리즘 트레이딩으로 진입할 때 아래의 델타헤지 조건으로 진입한 후 청산되기 전까지의 손익구조를 그린 것이다.

1) 콜옵션 X=277.5의 델타 = 0.303

콜옵션 X=280.0의 델타 = -0.215

2) 헤지 비율 = 0.303 / 0.215 = 1.4

3) 콜옵션 X=277.5 : 1 계약 매수     (10 계약 매수)

콜옵션 X=280.0 : 1.4 계약 매도   (14 계약 매도)

4) 합성 델타 : 0.002

합성 세타 : 0.027

초록색 사각형은 기초자산이 +- 1% 변할 때의 범위를 그린 것이다. 즉 기초자산인 KOSPI200이 269.73 ~ 275.18 사이일 때를 표시한 것이다. 기초자산이 이 범위에서 변동할 때 합성 그래프의 손익은 0.03 포인트 이내이다. 또한 합성 델타는 0.002에 불과하다 (0.303 – 1.4*0.215). 합성 델타가 작다는 의미는 기초자산의 변화에 따라 합성 포트폴리오의 손익 변화가 작다는 뜻이다. 따라서 이 포트폴리오로 만든 스프레드는 기초자산의 영향을 적게 받으므로, 일시적 괴리 (잔차)의 영향이 크다면 페어 트레이딩이 가능할 수도 있다는 의미가 된다.

기초자산이 +- 1% 사이에서 변동할 때 포트폴리오의 최대 변동폭은 0.03 포인트이고, 합성 세타는 +0.027이다. 이 의미는 기초자산이 변할 때 포트폴리오의 손익은 최대 0.03 포인트 하락하지만, 기초 자산의 1일 총 변화량이 없다면 약 0.03 포인트의 시간가치 (세타, +0.027)를 얻을 수 있는 상태로 최대 변동폭과 1일 시간가치가 서로 상쇄되는 의미가 있다. 이 상태는 일시적으로 보면 옵션의 양매도 전략과 유사한 상태가 된다.

이제 실제 스프레드가 위에서 예상한대로 움직이는지 확인하기 위해 아래의 시나리오로 실험해 보기로 하자.

* 델타헤지 페어 트레이딩 전략 시나리오 1. 알고리즘으로 인접한 행사가격의 두 옵션 (C1, C2)의 현재가를 실시간으로 감시한다. 2. 각 옵션의 델타값을 이용하여 헤지 비율을 계산한다. * 헤지비율 = C1의 델타값 / C2의 델타값 3. 각 현재가를 이용하여 스프레드를 계산한다. * 스프레드 = ln(C1) – 헤지비율 * ln(C2) 4. 실시간으로 스프레드의 이동평균 (균형점)과 표준편차를 계산한다.    5. 실시간으로 진입선과 청산선을 계산한다.      * 진입선 = 균형점 – 2*표준편차, 청산선 = 균형점 + 2*표준편차 6. 호가창의 매수/매도 가격이 진입선을 초과하면 진입한다. * 콜옵션 (C1) : 1계약 매수,  콜옵션 (C2) : 1*헤지비율만큼 매도 7. 호가창의 매수/매도 가격이 청산선을 초과하면 청산한다.

이전 포스트에서 사용했던 로봇으로 헤지비율만 조정하여 돌려보고, 로봇에서 수집한 로그파일을 이용하여 결과를 분석해 보면 스프레드가 위의 예상대로 어느 정도 정상성을 갖는지 확인할 수 있다. 결과는 다음 포스트에서 확인해 보도록 하겠다.

델타헤지에서 델타값은 N[d1]이므로, 델타값 자체가 기초자산의 변화에 영향을 받는다. 따라서 특정 시점에서의 델타헤지 비율은 기초자산에 따라 계속 변하게 된다. 스프레드가 완전히 기초자산 가격 변화에 대해 독립적이 되려면, 헤지비율을 연속적으로 바꿔주어야 한다. 즉, 동적헤지 (Dynamic Hedge)가 필요하다. 그러나, 동적헤지는 현실적으로 불가능하기 때문에 이로 인한 약간의 오차는 위험 요소로 작용할 수밖에 없다. 포지션 진입 이후 기초자산 변화에 따라 지속적으로 헤지비율을 맞추어 주려면 많은 거래 비용이 발생하므로 합리적이지 않다.

* 참고사항 (관심있는 분들만 보세요)

델타헤지 비율에 대해 수리적으로 해석해 보았다. 목적은 특정 시점을 기준으로 델타헤지를 하였을 때 위의 손익구조 그래프에서 정점에서 포지션을 잡게 되는지 확인하기 위해 수식을 전개해 보았다.

아래의 식 (1)은 두 콜옵션에 대한 블랙-숄즈 옵션 가격이다. 식 (2)는 델타헤지비율을 계산한 것이고, 식 (2)를 이용하여 두 옵션의 단순 가격차를 계산해 보면 식 (3)과 같이 된다. 델타헤지로 인해 두 옵션의 SN[d1] 부분이 서로 상쇄되어, 기초자산 S가 제거되었다. 그러나 d2 항속에 아직 S가 남아 있으므로, 완전히 제거된 것은 아니다. 식 (3)이 델타헤지를 적용한 페어 트레이딩의 단순 스프레드이다 (로그 스프레드는 아님).

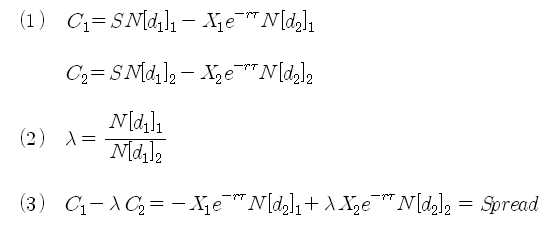
식 (3)의 스프레드가 기초자산 (S)의 변화에 대해 얼마큼 변화하는지 알아보기 위해 식 (4)와 같이 S에 대해 편미분을 해 보았다. 이 계산 과정은 N[d2]를 미분하는 과정이 필요한데, 이에 대해서는 금융수학/블랙숄즈 옵션공식의 미분 방법 [식 (9)~(11)]을 참조한다. (단, 람다는 상수로 취급)

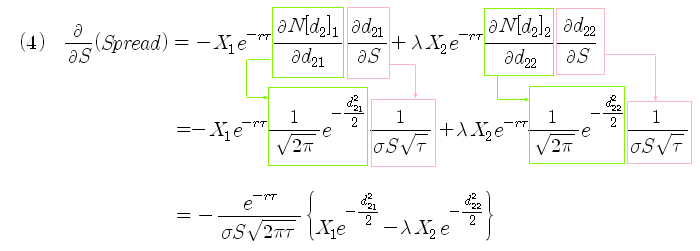
식 (4)의 최종식은 (정적) 델타헤지를 하였을 때 기초자산의 변화에 따른 스프레드의 변화량이다. 만약 델타헤지가 완벽하여 (그럴 리는 없지만), 스프레드의 변화가 전혀 없다면, 식 (5)와 같이 될 것이다. 여기서 람다는 델타헤지 비율로 이미 상수로 취급 하였지만, 이 식에서 람다를 다시 구해보면 식 (7)과 같이 된다. 위에서 사용한 조건을 이용하여 (2012.4.3일 현재 데이터), 식 (7)을 계산해 보면 1.20이 나온다. 이 값은 원래 사용했던 델타헤지비율인 1.41과는 약간의 차이가 난다.

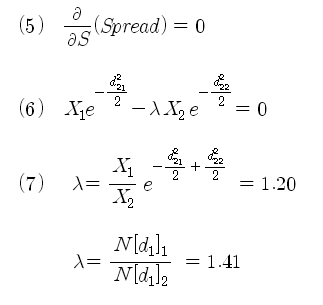
이 차이의 의미는 우리가 적용한 델타헤지가 합성 손익 그래프의 최고 정점에서 헤지를 한 것은 아니라는 의미이다. 정점은 아니지만 정점의 근처라는 것은 확인이 된 셈이다. 정점에서 헤지가 가능하도록 비율을 결정하려면 람다를 변수로 놓고 식 (1)에서부터 다시 미분하여 람다를 계산해야 되는데, 람다가 변수가 되면 SN[d1] 항 들이 소거되지 않은 상태에서 미분을 하게 되므로 식이 굉장히 복잡해진다. 필자는 이 식을 계산할 실력이 되지 않아 여기서 소개하지는 못한다. 그러나 식 (7)에서 근접한 결과를 얻었기 때문에 실무적으로는 델타헤지를 사용하여도 크게 무리는 없어 보인다.