News & Events
[Machine Learning] 40. 이상(사기) 탐지 : 또 다른 탐지 알고리즘 (Multivariate Gaussian Distribution)
- 2019년 1월 14일
- Posted by: 인사이트캠퍼스
- Category: 금융/AI/IT 기사

지금까지 배운 Anomaly Detection Algorithm은 Original Model 입니다. 가장 많이 사용되는 모델이지요
이번에는 비슷하지만 조금 다른 Multivariate Gaussian Distribution에 대해서 알아보겠습니다. variate의 의미는 허용이 가능한 어떤 집합이나 데이터의 그룹내에서 어떤 확률에 따라 데이터가 자유롭게 변수로 사용되는 것을 말합니다. 다시 이야기해보면 multivariate라는 의미는 어느 집합데이터 내에서만 추출이 되는 멀티 변수들이라고 생각하면 될 것 같습니다. 이에 대해서 하나씩 알아보겠습니다.
아래 그림과 같은 dataset이 있습니다. x1 에 대해서 오른쪽 상단의 그래프와 같이 정규분포를 형성하고 있습니다. 또 x2로 오른쪽 하단의 그래프와 같이 정규분포를 보입니다.
만약 녹색의 x 데이터가 있다고 생각해면, 왼쪽의 그래프에서는 비정상적인 데이터임을 눈으로 확인이 되지만 오른쪽의 x1, x2 의 분포상으로는 내부에 있기 때문에 anomaly detection이 안되는 문제가 발생할 수 있습니다. 이를 해결하기 위해서 새로운 feature를 추가했었지요
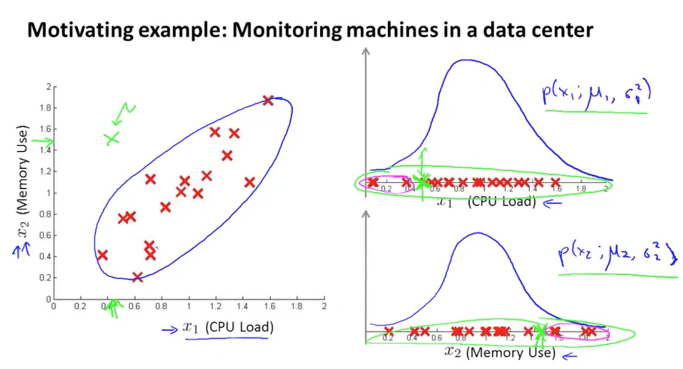
사실 그 원인은 아래와 같이 분포가 원의 형태로 존재하기 때문입니다. 결국 같은 분포상에 있는 녹색의 x 와 빨간색의 x가 동일시 되기 때문입니다.(오른쪽 그래프)

이것을 보완하기 위해서 나온것이 Multivariate Gaussian(Normal) distribution 입니다.
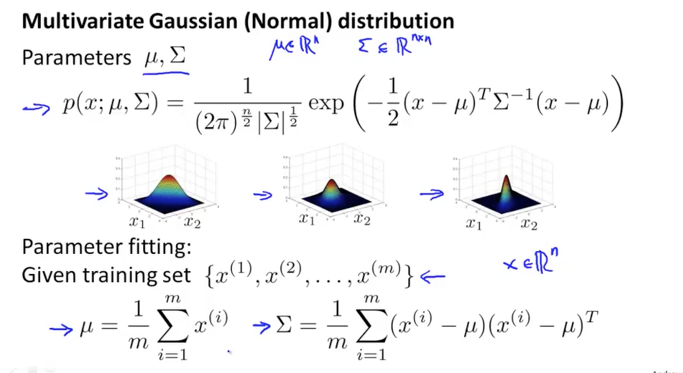
공식부터 살펴보면 아래 그림의 파란색 공식과 같습니다. 여기서 두가지 parameters가 나오는데 μ 는 n 개의 features를 의미하는 n-dimensional vector입니다. 그리고 Σ 는 n x n Matrix로 covariance matrix(공분산 행렬) 입니다.
그리고 |Σ| 은 sigma의 절대값으로 뒤에 나오는 sigma 값을 결정하는 값입니다. 이것은 Octave에서 det(sigma) 라는 명령어로 연산을 할수 있습니다.
복잡한 공식인데 이렇게 생겼구나만 보고 넘어가도록 합니다.

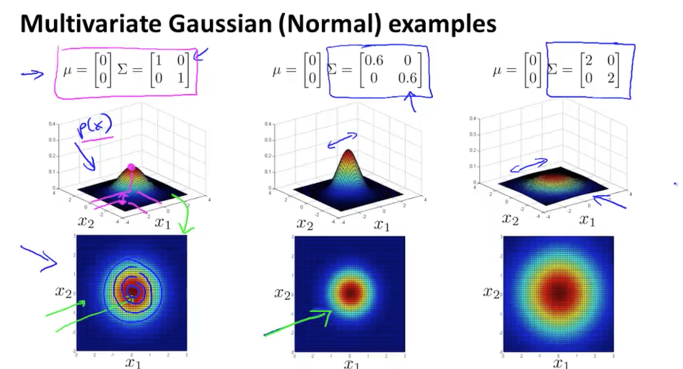
위 두개의 parameters가 의미하는 바를 그래프로 표현을 한 것입니다.
mu가 0으로 고정된 상태에서 sigma 값이 변함에 따라서 가우시안 분포의 모양이 달라지는 것을 볼 수 있습니다.
sigma 값이 작아지면 분포 원의 크기가 작아지면서 뽀죡해지고, 값이 커지면 원의 크기가 퍼지면서 커집니다.
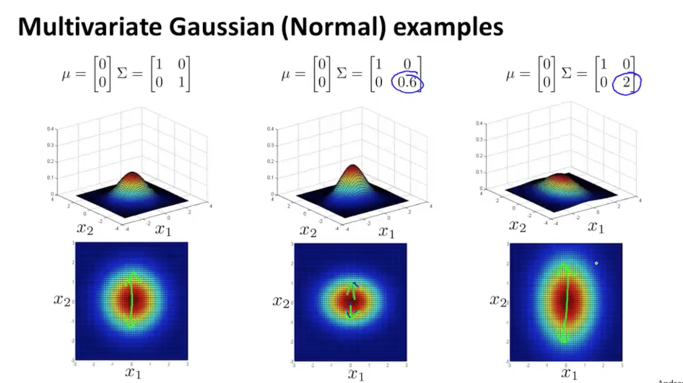
또 sigma의 x2값이 고정된 상태에서, x1 값이 작아지면 가로로 홀쪽한 모양이 되고, 값이 커지면 가로로 뚱뚱한 모양이 됩니다.
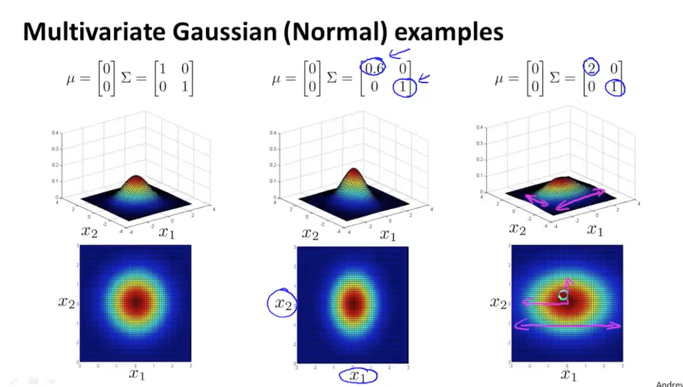
반대로 sigma의 x1값이 고정된 상태에서, x2 값이 작아지면 세로로 홀쪽한 모양이 되고, 값이 커지면 세로로 길쭉한 모양이 됩니다.
sigma의 대각선 0으로 고정되었던 값들이 값이 변하여 커질 수록, 대각선으로 홀쭉한 모양의 형태가 되고
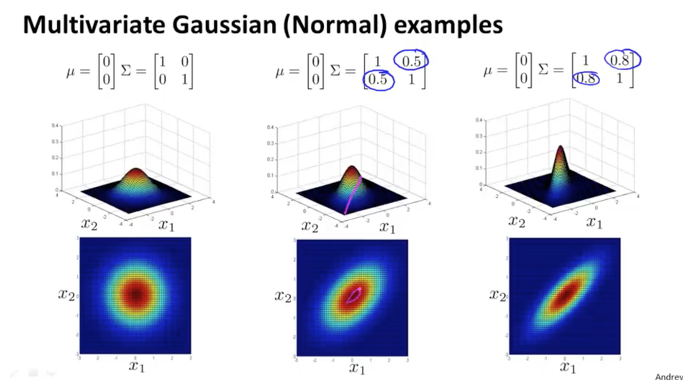
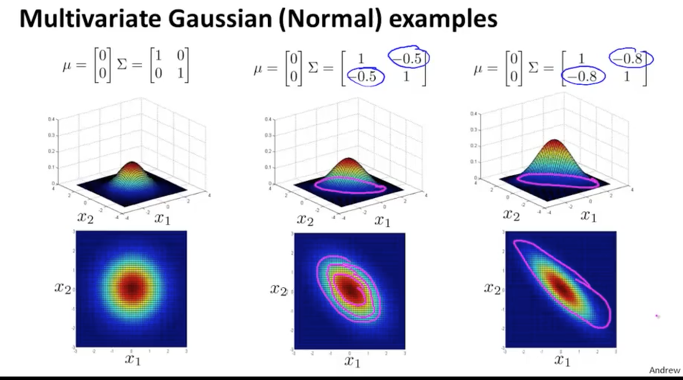
마이너스(-)의 값으로 커지면 반대 방향의 대각선으로 홀쭉한 모양의 형태가 되는 것을 알 수 있습니다.
이번에는 sigma 값이 고정된 상태에서 mu 값이 변하는 것을 보겠습니다.
x2의 값이 변하면 x2 축으로 이동을하게 되고(가운데 그림), x1/x2가 모두 변하면 중심점이 이동하는 것(오른쪽 그림)을 볼 수 있습니다.
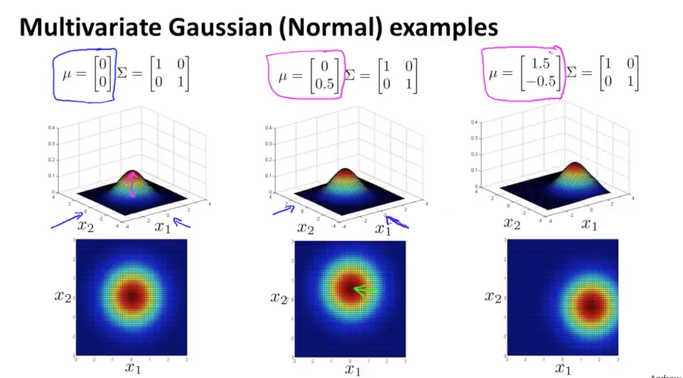
이렇게 두개의 parameter는 분포의 모양과 위치를 결정하는 변수들입니다.
지금까지 살펴본 공식을 정리하면 아래와 같이 됩니다. 그리고 두개의 parameter는 data의 평균과 거리를 통해서 값을 구할 수 있습니다.
지금까지 알아본 multivariate Gaussian distribution을 이용해서 anomaly detection에 적용해 보는 것을 살펴보겠습니다.
dataset을 통해서 mu와 sigma 값을 공식으로 구할 수 있었습니다. 이를 대입하면 p(x) 함수를 계산할 수 있게 됩니다. 이때 epsilon 보다 작은 p(x) 값을 가지는 것이 anomaly data가 될 것입니다.
이를 적용해서 오른쪽의 그래프와 같이 표현을 할 수 있습니다. 대각선 형태로 길쭉하게 생긴 형태가 됩니다. 이 분포상으로 봐도 눈으로 확인해도 녹색의 x는 anomaly data가 될 것 같습니다

Original model에서는 p(x) 공식이 아래와 같이 mu와 squared sigma들로 구성이 되었습니다. 이 Original model은 multivariate Gaussian model로도 동일하게 설명이 가능합니다. 하단의 multivariate Gaussian 공식에서 Sigma의 값이 하단의 matrix와 같이 구성이 된다면 Original model과 동일하게 될 수 있기 때문입니다.

하지만 이 두가지 모델은 다른 장단점을 가지고 있습니다. 아래 그림은 이를 비교해 놓은 것입니다.
Original Model은 보편적으로 많이 사용되는 algorithm 입니다. 그리고 기존의 features를 이용해서 새로운 featrure를 생성해주어야 하는 특징이 있습니다. 이것은 사람이 직접 생성을 해야하는 것이 risk로 작용할 수 있습니다. error analysis를 통해서 문제를 분석하고 이를 해결하는 과정이 필요하게 됩니다.
하지만 연산하는 비용이 저렴하기에 아주 많은 data를 처리하는데 용이합니다. features의 수인 n이 100,000으로 크더라도 수행하는데 부담이 없습니다. 바로 이런 장점 때문에 보편적으로 많이 사용이 되는 것입니다.
또 training set이 작은 경우에라도 잘 동작합니다. 100개 정도의 dataset만으로도 anomaly detection이 가능합니다.
Multivariate Gaussian Model도 자주 사용이 되기는 하지만 특정한 조건에서만 사용을 할 수 있는 제약이 있습니다. 하지만 Original model에서 수작업으로 해야 했던 new feature를 고려하지 않아도 되는 장점이 있습니다.
반면에 sigma의 inverse를 계산해야하기 때문에 연산 비용이 큽니다. sigma가 n x n 의 크기를 갖는 matrix 이고 다수의 연산이 필요하기 때문에 n의 값이 100,000이 되는 큰 dataset을 처리하는 것은 좋치 않습니다.
그리고 반듯이 m 이 n 보다 10배 정도 큰 dataset에서만 사용이 가능합니다. 만약에 n 이 큰 dataset에서는 사용될 수가 없는 것이지요
그리고 inverse 연산을 해야하기 때문에 sigma가 non-invertible 이 되면 안됩니다. 이를 방지하기 위해서는 중복된 features가 있다면 이를 찾아서 제거를 해주어야 합니다. (예, x2 = x1, x3 = x4 + x5 …)


