News & Events
[Machine Learning] 24. 뇌신경망을 이용한 머신러닝 (Neural Networks) 구성방안
- 2019년 1월 14일
- Posted by: 인사이트캠퍼스
- Category: 금융/AI/IT 기사

지금까지 NN에 대해서 하나씩 살펴봤는데요.
이번에는 전체적으로 정리하면서 살펴보도록 하겠습니다.
NN의 구성에 대해서 먼저 알아봅니다.
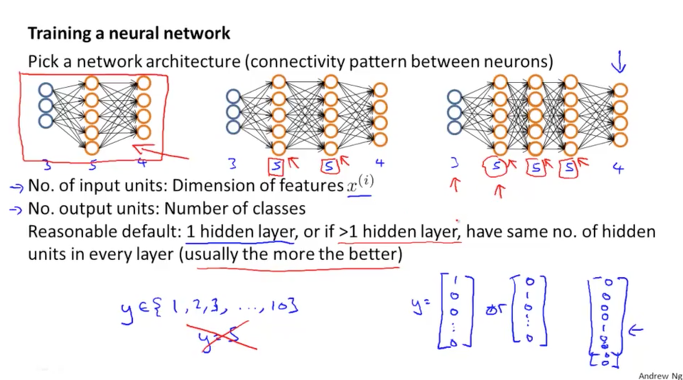
아래 그림과 같이 3가지 케이스의 NN이 구성되어 있습니다. 3가지 모두다 동일한 input, output activation을 가지고 있습니다.
다른점은 hidden layer가 첫번째는 1개, 두번째 구성은 2개, 세번째 구성에서는 3개를 가지고 있습니다.
Input units
NN을 구성할때 input units의 수는 자연스럽게 x features의 크기로 결정이 됩니다. 우리의 dataset이 가지고 있는 features들을 input 으로 주어야 하기 때문이지요
Output units
output units의 수는 어떻게 결정이 될까요. 마찬가지로 결과로 분류가 되는 classes의 수 만큼이 output이 될 겁니다. 먄약 y의 실제 결과값이 1부터 10까지라고 생각을 해봅니다. 그런데 NN에서의 구성에 따라 결과 h(x)가 [1; 0; 0; 0; 0]의 vector가 되는데 이때는 첫번째 class로 예측된다는 결과를 보여줍니다. 또 두번째 class로 예측된다면 [0; 1; 0; 0; 0]으로 나타나겠죠.
이때의 y는 5라고 생각하게 될 것입니다. 즉, NN이 5개의 결과로 분류를 한다고 생각하게 되겠지만 실제로는 10개중에서 5개만 분류하는 것일수도 있습니다.
결국 최종적으로는 h(x)의 값 뒤에 포함이 되지 않았던 나머지 5개 분류들을 0의 값으로 추가해서 y가 실제 class의 수만큼인 10개가 최종 결과가 되도록 할 수도 있겠습니다.
곧 이것은 결과를 위해서 반듯이 하나의 NN만으로 구성이 되지 않을 수도 있다는 의미가 됩니다.
Hidden units
그럼 이번에는 hidden layer는 어떻게 구성을 하는것이 좋은지에 대해서 알아보겠습니다.
기본적으로는 최소 1개의 hidden layer가 있어야 합니다. 그리고 hidden layer의 units의 수는 input units의 수에 배수로 지정하는 것이 좋습니다. 1.5배 혹은 2배~5배 이렇게 말입니다.
그리고 모든 hidden layers들은 같은 수의 units들을 가지고 있어야 합니다. 아래 3번째 구성과 같이 3개의 hidden layer들은 5개의 같은 수의 units을 가지고 있는 것과 같이 말입니다.
일반적으로는 hidden layer의 수가 많아질수록 더 좋은 결과를 보여주게 됩니다. 그런데 그에 반면에는 연산이 복잡해지므로 상대적인 비용이 커지게 됩니다. 학습 시간이 오래걸려 느려진다거나 하게 됩니다.
Implement Neural Network
NN의 구현하는 과정은 총 6개의 단계로 나누어 생각할 수 있습니다.
첫번째는 weight들에 대한 초기값을 랜덤하게 그리고 아주 작은 값으로 셋팅하는 것입니다.
두번째는 forward propagation의 방식으로 연산을 통해서 h(x)를 구할 수 있도록 구현을 하는 것입니다.
세번째는 J of theta의 cost 함수를 연산하는 것을 구현합니다.
네번째는 편미분을 계산하기 위한 back propagation 알고리즘을 구현하는 것입니다.
이때 for loop(반복문)을 사용하게 됩니다. 반복문 내에서 forward prop와 back prop을 구현하게 되는데요. 여기서 반복문을 사용하지 않고도 할 수 있는 인수분해와 같은 방법이 있긴 합니다만 이런 연산은 훨씬더 복잡한 계산을 하기 때문에 우리는 반복문을 사용해서 하는 것으로 합니다. 개념적으로 아래와 같이 구현이 될 것입니다.
for i = 1:m {
Forward propagation on (xi, yi) –> get activation (a) terms
Back propagation on (xi, yi) –> get delta (δ) terms
Compute Δ := Δl + δl+1(al)T
}

다섯번째는 gradient checking을 사용하는 것입니다. back prop를 사용해서 계산한 결과와 J of theta 함수의 기울기에 대한 수치적인 기울기의 결과와 비교해서 비슷하면 문제가 없으나 다르다면 back prop에 뭔가 문제가 있으니 체크를 해봐야 할 것입니다. 그리고 문제가 없다는 것이 확인이 되었으면 gradient checking을 비활성해줍니다.
여섯번째는 back prop를 사용해서 gradient descent나 advanced optimization들의 알고리즘을 수행하게 되면 J of theta 함수의 minimize 가 되는 parameters를 찾으려고 시도를 할 것입니다.
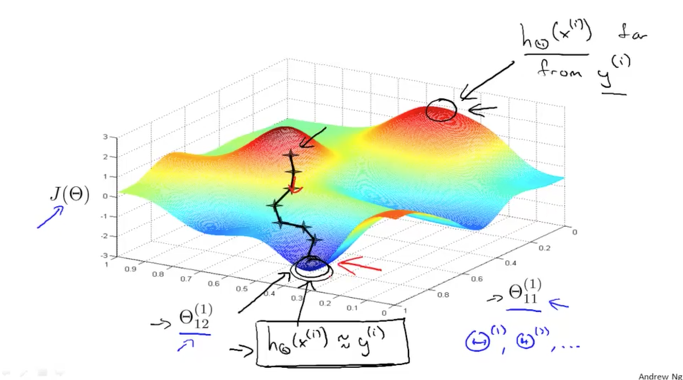
이때 J의 함수는 non-convex한 함수이기 때문에 여러개의 local minimum을 가지고 있을 것입니다 (맨 아래와 같은 그래프)
만약에 우리가 초기 weight(theta)의 값을 크게 주게 된다면 멀리있는 산봉우리에서 부터 내려오면서 다른 local minimum으로 갈 수 있습니다. 다시 우리가 초기 weight의 값을 작은 값으로 주게 된다면 우리가 원하는 가장 아래의 한점으로 global minimum을 따라 내려갈 것입니다. 이때 back prop는 경사를 따라 내려가야 하는 방향을 잡아주는 역할을 하게 됩니다.
이렇게 초기 값에 따라서 다른 결과가 나타날 수 있다는 사실을 염두해 두어야 하겠습니다.

여기까지 NN에 대해서 모두 알아보았습니다.
NN에서 사용되는 back prop 알고리즘등과 같이 복잡한 개념들이 있고, 교수님도 수년동안 사용해 오시면서 성공적인 결과를 도출해 내셨음에도 불구하고 아직까지 그 내부의 동작을 완전히 이해하지는 못한다고 하십니다. 하지만 이 back prop은 상당히 강력한 알고리즘이기에 오늘날에도 많이 사용되고 있고 특히 non-convex 함수에서 사용하기에 너무 좋은 알고리즘이라고 하니 유용한 넘인 것 같습니다.
NN은 많은 산업분야에서 유용하게 사용되고 있는데 특히, 무인 자동차, 자율운행 자동차에서 이 NN을 이용해서 실제 자동차가 사람이 운전하는 것을 통해 학습하고 도로 이미지를 통해서 자동으로 운전을 하도록 하는데 사용되고 있다고 합니다. 대단한 기술이 아닐 수 없습니다.

