[기술적분석] 11. KRE에 의한 주가 평활화

기술적 분석 (11) KRE에 의한 주가 평활화

기술적 분석에서 주가를 평활화 (Smoothing)하는 방법으로는 이동평균이 가장 많이 쓰인다. 이동평균선은 주가를 평균해서 만든 것이기 때문에 후행성이라는 특징이 불가피하게 나타난다. 또한, 후행성으로 인해 지지선과 저항선이 나타나는 특징도 보인다. 그렇다면 후행성이 전혀 없는 평할화 방법은 없을까? 하는 의문이 든다. 정답은 “없다” 이다. 과거의 데이터만을 이용하여 후생성이 없는 평활화 지표를 만드는 방법은 없다.

그러나 계산 시점에서 미래의 데이터를 이용하면 후행성이 없는 평활선을 만들어 볼 수는 있다. 여러 가지 방법이 있겠지만 여기서는 Kernal Regression Estimator (KRE) 라는 방법을 소개해 보기로 한다. KRE를 이해하기 위해서는 다소 수학적 배경이 필요하지만 여기서는 결과만을 언급하기로 한다.

KRE로 주가를 평활하는 식은 위의 공식과 같다. 이 식은 Kernal Function을 정의하여 임의의 시계열을 평활화하는 공식이다. x는 x-축의 값으로 순번 (1,2,3,4 …)을 나타내고, y는 y-축인 주가를 나타낸다. 그리고 h는 임의로 지정하는 값이다. h가 작을수록 평활화 정도가 작아지고 (단기 이동평균 같은), h가 클수록 평활화 정도가 커진다 (장기 이동평균처럼). 여기서 식 자체를 자세히 설명하는 것은 어려우므로 계산하는 방법에 대해서만 알아보기로 한다.

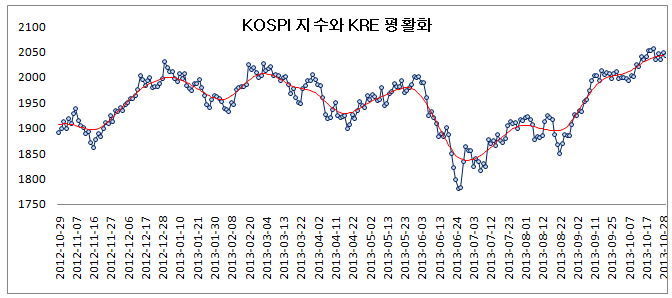
아래 그림은 약 1년간의 일별 KOSPI 지수를 대상으로 KRE를 계산한 것이다 (h = 5로 지정하였음). 상세 계산 방법은 VBA 코드를 참조 (첨부 파일 참조) 한다. 위의 식이 임의의 시계열에 대해 모두 성립하는 식이므로, 주가, 수익률, 변동성에 대한 KRE를 계산해 보았다.

B-열은 일별 KOSPI 지수를 나타내고, C-열은 주가의 일별 수익률을 계산한 것이다. D-열은 10일간 수익률의 표준편차를 계산하여 연간 단위로 환산한 수치로, 연간 변동성을 의미한다. 이 값들을 대상으로 KRE를 계산한 결과를 E, F, G 열에 표시하였다 (VBA 코드 참조)

결과를 확인하기 위해 그래프로 그려보면 아래 그림과 같다. 아래 그림은 KOSPI 주가 (B-열)와 주가의 KRE (E-열)를 그린 것이다. 빨간색 선이 KRE 선으로 주가의 평활선이다. 후행성은 전혀 보이지 않고, 주가를 잘 평활하고 있다.

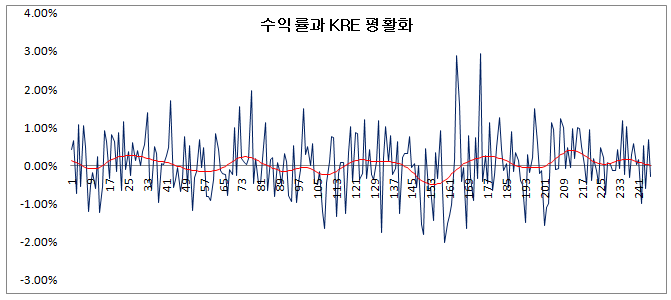
아래 그림은 수익률 (C-열)과 수익률의 KRE (F-열)를 그린 것이다. 수익률은 백색잡음과 같이 뾰족뾰족한 모양인데, 이를 평활화하면 빨간색처럼 완만하게 나타난다. 빨간선이 0% 보다 위에 있는 구간은 평균 수익률이 “+” 인 구간으로 주가가 오른 구간이고, 0% 보다 아래에 있는 구간은 평균 수익률이 “-” 인 구간으로 주가가 하락한 구간이다. 오실레이터 형의 기술적 지표들은 대부분 주가의 수익률을 설명하고 있다고 언급한 바 있다 (기술적 지표와 주가의 이동평균 수익률 참조).

아래 그림은 10일 평균 변동성을 평활화 한 것이다. 2013년 6월 까지는 변동성이 낮은 수준을 유지하다가 7월에 높아졌다가 그 이후 서서히 감소하는 모습을 볼 수 있다.

위의 그림에 보이듯이 KRE 선에는 후행성이 전혀 없다. 그러면 이동평균선 대신 KRE선을 사용하여 기술적 지표를 만들 수 있을까? 그렇다면 후행성이 없기 때문에 빠른 신호를 만들 수 있지 않을까? 그렇지는 않다.

그 이유는, KRE는 후행성이 없는 평활선이지만 계산 시점에 미래의 데이터를 이용했기 때문이다. 예를 들어, 5월 달의 KRE선은 그 이전 데이터와 이후 데이터를 모두 이용하여 계산하였다. 그러나 2013년 10월 22일의 KRE 선은 이후 데이터를 모르므로 이전 데이터만을 이용하게 된다. 즉, 기간에 따라 KRE 선에 이용된 데이터의 범위가 달라진다. 만약 매 시점마다 과거 데이터만을 이용해서 KRE를 그린다면 분명히 후행성이 나타난다. 그러므로 10월 22일의 KRE 선도 후행지표이고 이동평균과 유사해진다. 즉, 오른쪽으로 갈수록 후행성이 서서히 나타난다.

그러면 KRE 선은 어디에 활용해 볼 수 있을까? 가장 먼저 떠오르는 것으로, 과거의 패턴 분석에 이용할 수 있다. 주가 자체로 패턴을 분석하려면 뾰족뾰족한 부분이 너무 많아 패턴을 읽기가 불편하다. 이 때 KRE를 사용하면 분석이 용이해 진다. 예를 들어 과거 패턴 중에 헤드엔숄더 형이나 역-헤드엔숄더 형의 패턴을 검색할 때 활용될 수도 있고, 엘리엇의 파동을 해석하는 데도 활용될 수 있다. 물론, 이동평균선을 이용해도 동일하지만 KRE를 사용하는 것이 더 편리하다 (처음에는 복잡해 보이지만 코딩할 때 훨씬 편리함).

이상으로 KRE에 의한 주가 평활화 방법에 대해 알아보았다. KRE는 그 자체로는 큰 의미를 가지지는 않지만 여러 가지 분석을 할 때 편리한 도구로는 충분히 큰 의미를 가진다고 생각된다.

[출처]11. KRE에 의한 주가 평활화|작성자아마퀀트