[페어 트레이딩/고급편] 6. 스프레드와 정규분포

페어트레이딩 (Pairs Trading) – 고급(6)

스프레드와 정규분포   

페어트레이딩의 스프레드 차트는 정규분포의 특성을 나타낸다. 주식의 수익률과 같이 잔차의 성질을 가지고 있는 데이터들은 모두 정규분포의 특성을 갖는다 (정상 시계열). 따라서 스프레드가 정규분포에 가깝게 분포하고 있으면 잔차의 성질을 갖는다고 볼 수 있다. 스프레드가 잔차의 성질을 갖는다는 것은 한 쪽으로 발산하지 않고 (계속 오르거나 내리지 않고) 평균으로 회귀하는 성질이 있다는 것이다. 따라서 스프레드의 정규성을 확인해 보면 페어트레이딩에 적합한 것인지 간접적으로 알 수 있다 (직접적인 방법은 스프레드의 정상성에 대한 확인인데, 이 부분은 나중에 설명하겠다).

아래 그림은 삼성전자의 우선주와 보통주 간의 페어 차트이다 [그림-(가)]. 이 스프레드 차트에 대해 도수분포표를 그려 보면 아래 그림의 (나)와 같이 된다 (엑셀에서 히스토그램을 그리는 방법은 통계분석 팁의 1. (엑셀) 히스토그램 그리기 참조). 그림 (나)를 90도 회전 시키면 그림 (다)와 같이 스프레드 히스토그램을 얻을 수 있다.

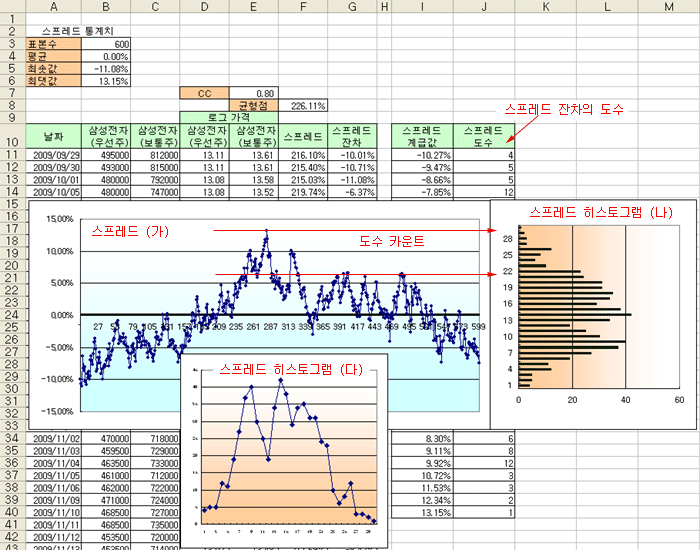
그림 (나)는 도수분포의 각 영역에 속하는(계급값) 스프레드들을 모두 카운트해서 그 개수만큼 막대그래프로 그린 것이다. 각 막대그래프의 꼭짓점을 연결하여 90도 회전시키면 그림(다)의 히스토그램을 얻을 수 있다. 그림(다)의 히스토그램이 정규분포에 가까운지를 확인하려는 것이다.

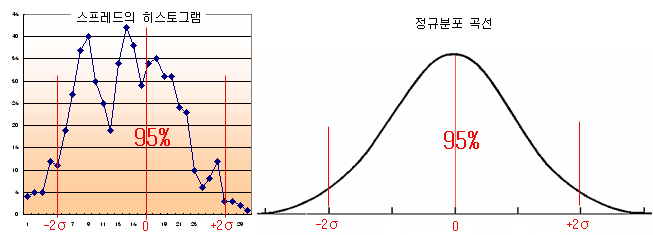
그림(다)의 히스토그램은 아래와 같이 정규분포 곡선과 약간 비슷한 것처럼 보인다. 평균점인 0 근처의 도수가 비교적 높다. 이것은 스프레드가 균형점 근처에 많이 몰려 있다는 것을 의미하고 평균점에서 균형을 이루었던 적이 많았다는 의미가 된다. 또한 평균점을 기준으로 좌,우로 대칭되어 있고, 평균점에서 멀어질수록 도수가 적게 나타난다. 이것은 균형점에서 멀어질수록 확률이 점점 낮아진다는 것을 의미한다. 표준 정규분포는 균형점을 중심으로 좌, 우의 2σ (표준편차의 2배) 되는 지점까지의 확률이 약 95% 정도 되는 것으로 알려져 있다. 이것은 스프레드가 이 범위에 속할 확률이 95%라는 의미이다.

스프레드가 속할 확률이 95% 되는 지점을 이용하면 진입선을 결정하는 데 참고가 될 수 있다. 아래와 같이 95%되는 지점을 선으로 이어 보면 (정확히 계산해서 그린 선은 아님), 스프레드가 이 범위에서 크게 벗어나지 않는다고 볼 수 있다. 따라서 스프레드가 이 범위를 벗어나면 진입선으로 활용해도 된다는 의미이다.

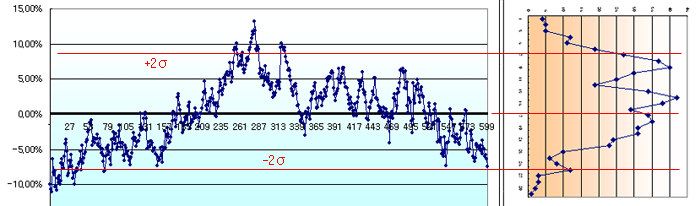
스프레드의 분포는 분석할 데이터의 기간에 따라 달라진다. 위의 스프레드는 2009.9.29 ~ 2012.2.22 까지 600일 간의 분석 결과인데, 만약 300일 간의 데이터로 분석하면 위와는 다른 히스토그램이 나올 것이다. 그러나 스프레드가 안정적이라면 어느 구간에서도 정규분포와 유사한 모양이 나와야 한다. 정규분포의 모양을 하고 있지 않으면 페어가 잘못 선정되었을 가능성이 높다.

스프레드의 분포가 정규분포에 해당하는지를 통계적으로 엄격히 판단하려면 정규성 검정 절차를 거쳐야 한다. 그러나 실전에서는 육안으로만 확인해도 충분하다. 정규성 검정 절차를 거치려면 유의확률 (p-value)을 구해서 유의 구간에 해당하는지를 판단하는 것인데, 확률이 약간 차이가 난다고 해서 실전에서 크게 달라지는 것은 별로 없기 때문이다 (정규성 검정 절차에 대해서는 다음 포스트에 설명하도록 하겠다).

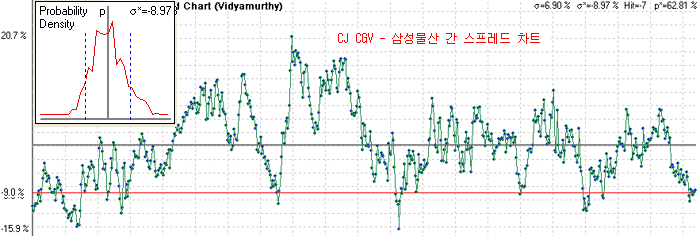
히스토그램에 대해 몇 종목의 실례를 들어 보자. 아래 그림은 CJ CGV와 삼성물산 간의 스프레드 차트이다. 왼쪽에 보이는 것이 스프레드의 히스토그램이다. 평균점 부근에 도수가 많이 분포해 있고, 정규분포에 가까운 분포를 하고 있다. 스프레드 차트도 균형점을 중심으로 상당히 안정적인 모양을 하고 있다. 따라서 이 종목에 대한 페어트레이딩은 별 무리가 없어 보인다.

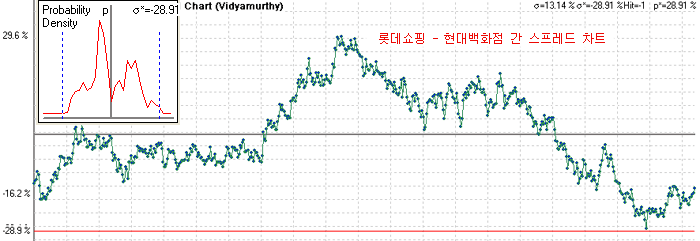
아래의 예는 롯데쇼핑과 현대백화점의 스프레드 차트이다. 스프레드의 히스토그램을 보면 균형점 부근의 도수들이 매우 적게 분포해 있고, 균형점에서 멀리 떨어진 지점에 많이 분포하고 있음을 알 수 있다. 스프레드 차트를 보아도 평균으로 회귀하는 성질이 낮아 보이고 주기도 길어 보인다. 이 기간의 그림으로만 봐서는 일단은 페어트레이딩에 적합하지 않은 것으로 보인다.

이상으로 스프레드에 대한 정규분포 특성을 간단히 살펴보았다. 다음 편에서는 통계적 방법에 의해 스프레드의 정규성을 검정해 보겠다. 꼭 필수적인 절차는 아니지만 페어트레이더라면 한 번쯤은 해 보는 것도 좋을 것이다.

[출처]6. 스프레드와 정규분포|작성자아마퀀트