[페어 트레이딩/기초편] 18. 차익거래의 종류

페어트레이딩 (Pairs Trading) – 기초(18)

차익거래의 종류  

 오늘은 잠깐 쉬어가는 차원에서 가벼운 주제로, 페어트레이딩이 차익거래의 분류상 어디쯤 속하는지 살펴보고자 한다. 차익거래의 다양성으로 인해 제대로 분류하기는 어렵지만 나름대로 분류해 보았다.

시장에 존재하는 차익거래 (재정거래)의 종류는 무수히 많다. 특성별로 분류하기가 어려울 정도로 종류가 다양하다. 그 이유는 현대의 금융 시장은 너무도 다양하고 유기적인 관계로 복잡하게 얽혀있기 때문이다. 복잡한 관계 속에서 일물일가의 원칙이 깨진 곳에서는 차익거래 기회가 발생할 수밖에 없고, 차익거래를 통해 복잡한 금융 시장이 안정되어 효율적 시장이 형성되는 것이다.

차익거래를 크게 세 분류로 아래 그림과 같이 분류해 보았다. 위험이 거의 없는 무위험 차익거래, 위험을 수반하는 차익거래 그리고 약간의 통계적 위험을 수반하는 통계적 차익거래가 있다. 위의 세 경우 모두 페어 롱/숏으로 접근하는 전략이다. 페어트레이딩이란 말도 롱/숏 페어이므로 위의 모든 경우를 페어트레이딩이라 할 수도 있지만, 통상적으로 페어트레이딩은 주로 통계적 차익거래의 의미로 사용된다. 페어트레이딩은 수많은 차익거래 중에 극히 일부분에 해당하며, 분류상으로는 통계적 위험을 수반하는 통계적 차익거래에 해당한다.

1. 무위험 차익거래 (Risk Free Arbitrage)

무위험 차익거래는 위험 수준이 거의 0인 안전한 차익거래를 말한다. 대표적인 것으로는 현-선물 차익거래가 있다. 선물과 (Futures) 기초자산인 주가 지수의 (KOSPI200) 가격 괴리를 이용하여 무위험 차익을 실현하는 것이다. 여러 종목의 대형주를 하나의 바스켓으로 묶어서 주가 지수를 복제한 다음 선물 가격과 비교하여, 가격이 낮은 쪽을 매수하고 가격이 높은 쪽을 매도하는 전략이다 (현물 바스켓과 선물을 페어로 보면 이것도 페어트레이딩이라 할 수 있다).

만약 현재 선물가격이 높고 주가 지수가 낮다면 선물을 매도하고 주가 지수를 매입할 수 있다 (바스켓에 속한 종목들을 매입). 주가 지수를 매입하므로 매수 차익거래라고 한다. 매수 차익거래의 진입과 만기 청산 시 손익 (Pay Off)을 따져 보면 아래 테이블과 같이 된다 (거래비용 및 배당효과는 고려하지 않고 단순하게 살펴본다).

* FM – 시장 선물 가격

SM – 시장 현물 가격 (KOSPI200)

ST – 만기 시 현물 가격

r – 차입 이자율 (무위험 이자율, 실무적으로는 CD 금리를 적용함)

FM – SM : 시장 베이시스

선물이 KOSPI200 지수 보다 높으므로 선물을 매도한다. 선물 매도 계약 시에는 현금 흐름이 발생하지 않으므로 진입 시 손익은 0이 된다. 반대로 현물은 매수한다. 현물 매수 시에는 SM 만큼 현금이 나가므로 초기 손익은 -SM이 된다. 그 다음은 현물을 매수할 현금을 머니 마켓에서 차입한다. 이렇게 하면 초기의 총 손익은 0이 된다. 차익거래의 기본은 초기의 현금 흐름이 0이어야 한다는 점이다. 즉, 투자비용이 없다는 뜻이다.

만기가 되면 선물은 매수 청산되어 만기 손익은 (FM – ST)가 된다. 차입한 현금도 갚아야 하므로 -SM*(1+r)의 현금 흐름이 발생한다. 초기에 매수한 현물은 가격이 변하여 ST가 된다. 따라서 만기 시 총 현금 흐름은 FM – SM*(1+r)이 된다 (차입 이자율 r은 연 이자율에서 해당 기간 만큼의 이자율로 환산해야 한다).

초기 투자비용이 0이므로, 만기 손익이 0보다 크다면 차익이 발생하는 것이다. 즉, 아래 식과 같이 시장 베이시스가 r*SM 보다 큰 순간을 포착하면 차익거래를 실현할 수 있다.

차익거래 조건 : FM – SM*(1+r) > 0  —> FM – SM > r*SM

시장베이시스 > r * SM    (거래비용 및 배당효과는 무시한 경우)

하지만 바스켓으로 KOSPI200을 복제할 때 발생하는 오차 (Tracking Error) 등이 있기 때문에 무위험 차익거래라고 해서 위험이 완전히 0이 되는 것은 아니다.

선물 대신 기초자산이 같은 옵션을 합성하여 선물을 복제할 수도 있다. 풋-콜-선물 패리티를 이용하면 (식-1)과 같이 되어 콜 옵션을 매입하고, 풋 옵션을 매도하면 선물을 매입하는 것과 동일한 효과를 낼 수 있다 (여기서 채권은 두 옵션의 가격차인 프리미엄의 차가 된다). 콜과 풋으로 합성한 선물과 실제 선물의 가격차가 발생하면 차익거래가 가능하게 된다.

콜 매입 + 풋 매도 = 선물매입 + 채권   — (식-1)

만약 합성 선물이 실제 선물보다 비싸다면 합성 선물을 매도하고 실제 선물을 매입하면 된다 (Conversion). 반대로 합성 선물이 실제 선물보다 싸다면 합성 선물을 매입하고 실제 선물은 매도하면 된다 (Reverse Conversion). [그림-1]의 (가)와 같이 실제 선물 – 합성 선물 – 주가 지수 간 베이시스를 관찰하여 가장 큰 차익 기회를 포착하면 유리할 것이다.

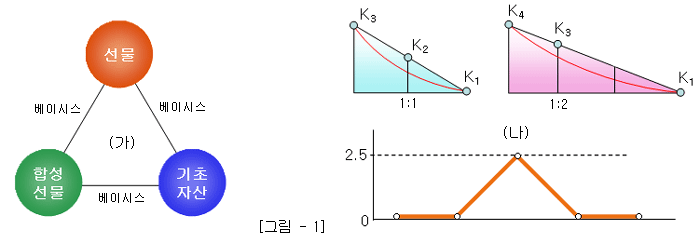
또 다른 예로는 옵션의 행사가격 간의 괴리를 이용한 차익거래도 생각해 볼 수 있다 (Options Strike Arbitrage). 옵션에는 블랙-숄즈 방정식으로부터 유도한 “행사가격에 대한 옵션가격의 민감도”라는 Greeks가 있는데, 이로 인해 행사가격 간에는 이론적인 가격차가 존재한다. 이 이론적인 가격차가 정상 범위를 벗어나면 차익거래가 가능한 것이다.

예를 들어 [그림-1] (나)의 하늘색 삼각형을 보자. 삼각형 빗변에 3개의 행사가격 (K1, K2, K3)이 있는데, 행사가격 민감도에 따라 계산해 보면, 각 행사가격의 적정 가격은 빨간색 곡선을 따라 분포한다. 만약 행사가격 K2의 옵션 가격이 빨간 선 이상의 점에 있다면 차익거래가 가능하게 된다. 삼각형의 비례식을 적용해 보면 근사적으로 2*K2 = K1 + K3 이므로, 행사가격 K2인 옵션을 2계약 매도하고 행사가격이 K1, K3인 옵션을 각각 1계약씩 매수한 후 만기를 기다리면 만기 손익 그래프는 그 아래 그림과 같이 된다. 즉, 만기 손익이 전 구간에서 양(+)의 값이므로 만기 주가에 상관없이 0 ~ 최대 2.5 포인트 사이의 차익을 얻을 수 있다. 참고로, 보라색 삼각형의 경우처럼 인접 행사가격이 아닌 한 칸 떨어진 행사가격의 옵션을 이용하면 3*K3 = 2*K1 + 2*K4가 되어 차익은 더욱 커지게 된다.

행사가격 차익거래는 매우 순간적으로 발생할 수 있으므로 (실제로는 거의 포착하기 어렵다), 알고리즘 트레이딩 (시스템 트레이딩)의 영역이 된다. 요즘은 시스템들이 자동으로 차익거래 기회를 계속 포착하여 즉시 실현하므로 괴리가 거의 발생하지 않는다. 반면에 시장은 그 만큼 효율적이 되는 것이다.

2. 통계적 차익거래 (Statistical Arbitrage)

두 금융 자산의 가격차 (스프레드)가 균형점에 수렴하는 특성을 이용한 차익거래이다. 균형점으로 수렴하는 특성이 확률적이기 때문에, 예측이 벗어나면 손실을 볼 수 있는 차익거래이므로 통계적 차익거래라고 한다. 우리가 그 동안 살펴본 페어트레이딩이 대표적인 경우이다. 그 동안의 설명으로 부가적인 설명은 생략한다.

3. 위험 차익거래 (Risk Arbitrage)

어떤 기업에 특별한 이벤트가 발생할 때를 이용한 차익거래가 대표적인 경우이다 (Event Driven Arbitrage). 기업의 이벤트는 기업 합병 (M&A)이나 자본 구조 변경 등이 있을 수 있는데, 여기서는 기업 합병의 예를 들어 보기로 하자. 아래 그림처럼 기업-A가 기업-B를 흡수 합병 하려고 한다. A-기업은 B-기업의 주주들에게 합병의 대가로 A-기업의 주식을 교환 비율 0.5로 지불하기로 하였다고 가정한다.

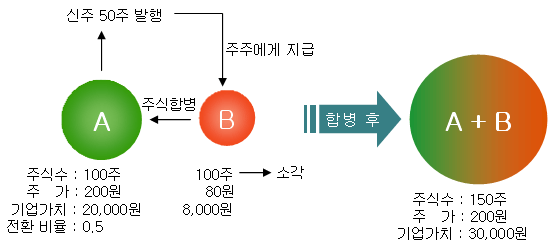
A-기업은 신주 50주를 신규로 발행하여 B-기업의 총 주식 수 100주의 대가로 지불하고, B-기업의 주식 100주는 소각 처리 한다 (교환 비율이 0.5이므로 50주 발행). 합병 전 두 기업 가치의 합은 28,000원이고, 합병 후 A+B 기업의 가치는 30,000원이 된다. 합병 후 2,000원 이상의 합병 시너지 (Synergy)가 발생한다면 충분히 합병의 효과를 볼 수 있다.

위와 같은 합병 계획이 발표되었다면 (혹은 정보를 입수하였다면), B-기업의 주식은 20원 만큼 오를 것이므로, B-기업의 주식 2주를 매수한다. 반대로 A-기업의 주식 1주를 매도한다. 여기서 헤지 비율은 주식의 교환 비율이 된다. 합병 후 A+B 기업의 주가가 그대로 200원이 된다면 40원의 차익을 얻을 수 있다. B-기업의 주식 2주 (160원)가 소각되는 대신 A-기업 주식 1주 (200원)를 받았으므로 차익은 40원이 된다.

만약 합병 후 시장에서 합병의 효과를 부정적으로 보아 A+B 기업의 주가가 180으로 하락하였다면, A-기업 주식 1주 매도한 것에서 20원의 이득이 발생하고, B-기업의 주식 2주를 매수한 것에서 20원의 이득이 발생하므로 총 40원의 차익이 발생한다. 페어로 구성하였으므로 합병 후 A+B 기업의 주가에 상관없이 일정한 차익이 발생하는 것이다.

그러나 합병 계획 발표 후 최종 합병이 이루어지지 않을 경우에는 차익을 기대할 수 없고, 위험에 노출되게 된다. 따라서 이러한 형태의 차익거래를 위험 차익거래 (Risk Arbitrage)라고 한다.

이상으로 몇 가지 경우의 차익거래를 살펴보았다. 실제로는 위에서 설명한 차익거래 이외에도 무수히 많은 차익거래가 존재한다. 채권, 외환, 금리, 상품 시장 등 모든 금융 시장에서 차익거래 기회가 있을 수 있다.

위에서 살펴보았듯이 모든 차익거래가 롱/숏, 즉 페어로 구성되어 있음을 알 수 있다 (예외의 경우가 혹시 있을지는 모르겠지만). 이런 측면에서 보면 페어트레이딩이라는 말이 단지 통계적 차익거래만을 지칭하는 것이 아니라, 모든 차익거래를 포괄하는 개념으로도 볼 수 있다.

[출처]18. 차익거래의 종류|작성자아마퀀트