News & Events
[알고리즘 트레이딩/시장미시구조] 33. PIN 모형 (9) – 매수 매도의 불균형 분포
시장미시구조론 (Market Microstructure) – (33)
PIN 모형 (9) – 매수 매도의 불균형 분포
PIN 모형은 매수와 매도 거래의 불균형 정도를 측정하여 시장에 유입된 정보량을 추정한다. 특별한 정보가 없다면 매수와 매도는 균형을 이룰 것이고, 호재성 정보가 있다면 매수가 강하고, 악재성 정보가 있다면 매도가 강할 것이다. 정보를 알지 못하는 비정보기반 거래자는 (Uninformed trader) 매수와 매도의 불균형 정도를 측정하여 역으로 정보를 추정한다.
매수와 매도의 불균형 정도를 단위 시간당 매수 수량과 매도 수량의 차이 (d = B – S, B=Buy, S=Sell)로 나타내보자. 차이 (d)가 0 에 가까우면 매수와 매도가 균형 상태에 있는 것이고, d > 0 이면 매수가 강하고, d < 0 이면 매도가 강한 것이다. 아래 그림은 2014.06.24. (09:00:00 ~ 14:50:00) SK-하이닉스의 5분봉 데이터이다. 매수 수량과 매도 수량의 차이 (B-S)를 5분 간격으로 측정하였다. 09:00:00 ~ 09:05:00 에는 B-S = 30,711 로 매수가 강했고, 그 다음 시간대에는 B-S = -14,154로 매도가 강했다.
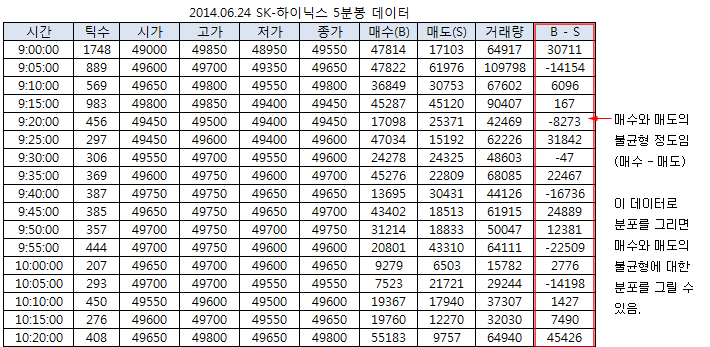
위의 데이터를 이용하면 하루 전체의 B-S 에 대한 분포를 그려볼 수 있다. 이 분포가 0 부근에 많이 몰려 있다면, 이 날은 정보가 없었을 가능성이 큰 것이고, 우측 (+) 분포가 넓다면 호재성 정보가, 좌측 (-) 분포가 넓다면 악재성 정보가 있었을 가능성이 큰 것이다.
참고로, 매수 (B)와 매도 (S)는 포아송 분포를 따르고, 그 차이인 B-S는 포아송 분포의 차이인 Skellam 분포를 따른다. 위의 데이터는 5분 간격으로 측정 시간이 짧아 매수와 매도 사건이 독립적이라고 보기는 어렵지만, 여기서는 독립이라고 가정한다.
아래 그림은 하루 동안 B-S 의 분포를 그린 것이다 (09:00:00 ~ 14:50:00). 좌측 분포는 위의 자료를 이용한 것이고, 우측 분포는 2014.06.27 데이터를 이용한 것이다. 좌측 분포는 대략 0 을 중심으로 (약간 + 지점을 중심으로) 좌, 우로 퍼져있고, 우측 분포는 (-) 지점을 중심으로 좌, 우로 퍼져있다.
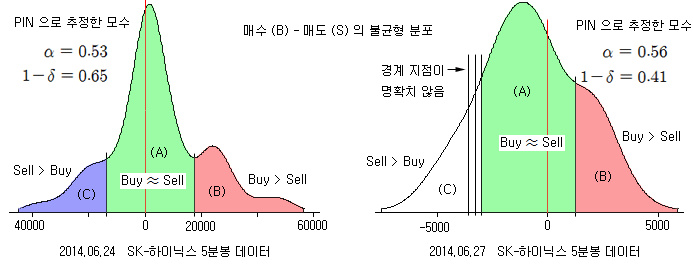
좌측 분포는 전체적으로 (+) 영역이 약간 넓다. 즉, 매수 강도가 매도 강도보다 높은 경우가 많았다 (Buy > Sell). 반대로 우측 분포는 (-) 영역이 넓어 매도 강도가 높았다 (Sell > Buy). PIN 모형에 의하면 이 분포는 3개의 Skellam 분포의 결합 분포로 이루어져 있다 (A, B, C). (A) 영역은 정보가 없을 확률을 의미하고 (1-α), (B) 영역은 정보가 있는 경우 (α) 호재성 정보일 확률을 의미한다 (1-δ). 그리고 (C) 영역은 정보가 있는 경우 (α)에 악재성 정보일 확률을 의미한다 (δ).
PIN 모형으로 좌측 분포를 추정해보면 α=0.53, 1-δ=0.65 이다. 정보가 존재할 가능성이 53%로 정보가 없을 가능성보다는 높고, 호재성일 가능성은 65%이다. 이 결과는 (+) 영역이 넓은 것과 잘 일치한다. 우측 분포는 α=0.56, 1-δ=0.41 로 정보가 있을 가능성이 높고 (56%), 악재성 정보일 가능성이 높다 (59%). 이 결과도 (-) 영역이 넓은 것과 잘 일치한다.
좌측 분포를 자세히 보면 (A)와 (B) 사이, 그리고 (A)와 (C) 사이의 경계가 잘 나타난다. 경계선을 그려 놓고 보면 분포의 모양과 PIN 모수 (Parameters)들의 관계를 쉽게 알 수 있다. (A)의 면적은 α를 의미하고, (B)의 면적은 α(1-δ)를 의미한다. 그리고 (C)의 면적은 αδ를 의미한다. PIN 모형의 MLE 추정은 바로 이 경계를 찾는 과정이라고 볼 수 있다.
우측 분포는 (A)와 (B)의 경계는 약하게나마 나타나지만 (A)와 (C)의 경계는 잘 나타나지 않는다. 육안으로는 확인이 잘 안되지만 MLE로 추정하면 그런대로 경계를 표시해볼 수 있다 (추정 오차가 크다고 할 수 있을까 ??).
여기까지의 관찰로 흥미로운 사실을 알 수 있다. 위에서 언급한대로 PIN MLE로 추정한 α와 δ를 이용하면 위의 분포를 3개의 영역으로 나누는 경계를 표시할 수 있다. 그렇다면 어떤 방법으로든 경계만 정할 수 있다면, MLE를 사용하지 않고도 α와 δ를 추정할 수 있다는 것을 알 수 있다.
이 아이디어는 2014년 Quan Gan, David Johnstone, Wang Chun Wri 이 제안한 것이다. Wang Chun 등은 위의 분포를 3개의 Cluster로 구분해서 α,δ, μ, ε을 추정하는 Cluster PIN (CPIN) 모형을 소개하였다. CPIN은 데이터 사이언스 (머신 러닝, 데이터 마이닝 등)의 Clustering (군집화) 기법을 이용하여 위의 분포를 3개 영역으로 나눈 후 PIN의 모수들을 계산한다. CPIN은 MLE를 사용하지 않으므로 계산 속도가 대단히 빠르다. 따라서 방대한 데이터를 이용한 실증분석이나, PIN 모형을 이용한 단기 매매 전략에 매우 유용하게 사용할 수 있다. CPIN에 대해서는 다음 포스트에서 자세히 다루기로 한다.
