[알고리즘 트레이딩/시장미시구조] 19. 호가창 포아송 분포의 시뮬레이션

호가창 분석 (7)

호가창 포아송 분포의 시뮬레이션

전략개발 및 테스트를 위해서는 시뮬레이션 방법이 매우 효과적이다. 이번 시간에는 호가창에 대한 포아송 분포의 시뮬레이션 방법에 대해 알아본다. 포아송 분포를 시뮬레이션 하려면, 아래 식에서 확률 p 에 0 ~ 1 사이의 랜덤 값을 대입한 후, 확률변수 (Random Variable)인 x (단위 시간당 사건의 발생횟수) 를 만들어 내면 된다. 평균 발생횟수인 Lamda는 시장에서 측정할 수 있으므로, 시장의 사건 발생에 대한 시뮬레이션을 만들어 볼 수 있는 것이다. 그러나 아래 식으로 x에 대해 정형화된 식 (Closed-form)을 만들기는 어려워 보인다.

정형화된 식을 구하기 어려울 때 사용할 수 있는 방법으로는 수치해석이 있다. 수치해석으로는 당연히 주어진 확률 p에 대한 확률변수 x를 구할 수 있을 것이다. 다른 방법으로는 지수 분포를 이용하여 포아송 분포의 시뮬레이션을 만들어 볼 수도 있다. 이전 시간에 언급한 바 있지만, 포아송 분포와 지수분포는 서로 밀접한 관계가 있고, 지수 분포에서는 Closed-form으로 확률변수인 x를 구해낼 수 있다. 따라서 지수분포를 잘 활용하면 수치해석을 이용하지 않고도 포아송 분포의 시뮬레이션을 만들어 낼 수 있다.

지수 분포를 이용한 방법은 향후 포스트에서 살펴보기로 하고, 이번 포스트에서는 단순히 반복 실험을 통해 포아송 분포를 시뮬레이션 해 보기로 하겠다. 이전 포스트의 예제에서 살펴본 대로, 평균적으로 10초당 47건의 시장가 매도 주문이 유입되는 상황에 대해 시뮬레이션을 해 보자.

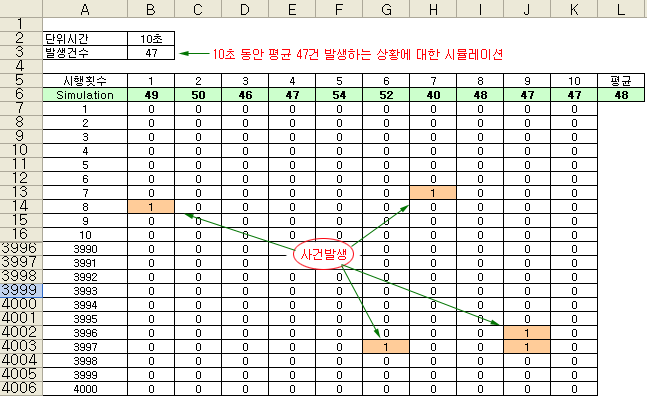
1회 실험을 4,000번 수행하기로 하고, 매 번 실험에서 사건이 발생하면 “1”, 발생하지 않으면 “0” 으로 판단해 보기로 하자. 그러면 47을 4,000으로 나눈 값인 0.01175 라는 숫자를 활용할 수 있다. 0 ~ 1 사이의 난수를 발생하여, 이 값이 0.01175 보다 작으면 사건이 발생한 것이고, 0.01175 보다 크면 사건이 발생하지 않은 것으로 판단해 본다.

셀 B7 ~ B4006 : = if(rand() < $B$3 / 4000, 1, 0)

셀 B6 := sum(B7:B4006) <– 1회 실험에서 발생한 총 사건의 개수

열 C ~ K : 열 B와 동일

위의 식으로 각 셀을 만들어 총 10회 실험을 수행해 보면, 위 그림과 같은 시뮬레이션 결과를 얻을 수 있다. 1회 실험에서 발생한 사건은 49건이었고, 2회 실험은 50건, 3회 실험은 46건 등 이다. 총 10회까지의 평균 발생사건은 48건으로 주어진 47건과 유사한 값을 얻을 수 있었다. 이와 같은 방법으로 실험의 횟수를 증가시키면 포아송 분포를 시뮬레이션 해 볼 수 있다.

이번에는 위의 방법을 확장하여 총 4,000번의 실험을 반복 수행해 본다. 아래와 같이 VBA 코드를 이용하여 매회 4,000번씩 사건발생의 유, 무 (1 or 0)를 실험하고, 이 실험을 또 4,000번 반복하여 총 4,000번의 사건 발생횟수를 만들어 본다.

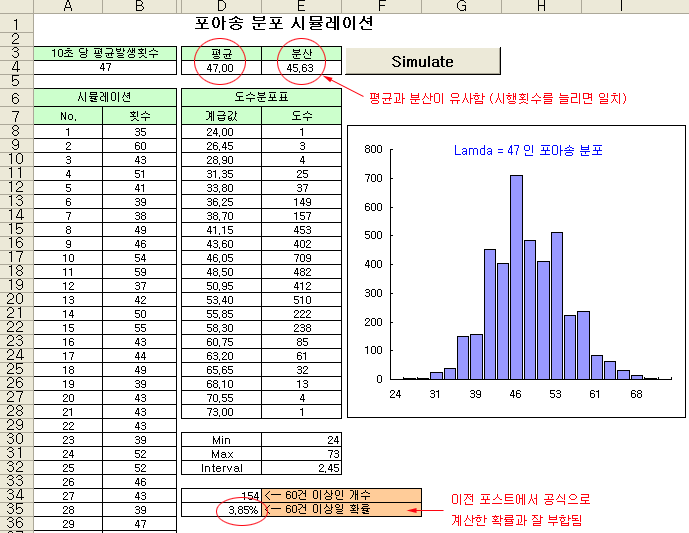
위의 코드로 만들어진 시뮬레이션 결과는 아래 그림과 같다. 평균 발생횟수가 10초당 47건인 상황에서, 첫 번째 실험에서는 35개 (셀B8)가 발생하였고, 두 번째 실험에서는 60개 (셀B9)의 사건이 발생하였다. 평균은 47.00 번이 발생하였고, 분산은 45.63 이었다. 평균은 주어진 47회와 잘 일치하고 있다. 또한, 평균과 분산이 유사한 것으로 보아, 시뮬레이션 결과가 포아송 분포에 가깝다는 것을 알 수 있다. 실험횟수를 4,000 번 이상으로 늘리면 평균과 분산은 더 가깝게 일치할 것이다. 히스토그램을 보면 평균이 큰 포아송 분포의 형태를 띠고 있다.

위의 시뮬레이션 결과로 이전 포스트에서 다루어본 아래의 예제를 다시 생각해 본다.

Q3) 최우선 매수 호가창의 현재 잔량이 60개 이고, 내 주문이 60번째에 있다면, 내 주문이 10초 이내에 체결될 확률은 얼마인가? (단, 10초 동안 Mid-price의 변화와 취소 주문은 없다고 가정한다.)

A3) 평균적으로 10초 동안 47개의 시장가 매도 주문이 발생하는 상황에서, 10초 이내에 내 주문이 체결되려면, 10초 동안 60개 이상의 시장가 매도 주문이 발생해야 한다. 위 시뮬레이션 결과에서 발생 횟수가 60개 이상이 되는 경우를 카운트해 보면 154건이다. 총 실험횟수는 4,000번 이므로, 발생확률은 154/4000 = 3.85% 이다.

셀 D34 : = COUNTIF($B$8:$B$4007,”>=60″)

셀 D35 : = D34 / 4000

위의 결과와 같이 10초 이내에 60개 이상의 시장가 매도 주문이 유입될 확률은 3.85%로 시뮬레이션 되었다. 이것은 이전 포스트에서 수식으로 계산한 확률인 3.81%와 잘 일치한다.

이번 시간에는 간단히 반복 실험만으로 포아송 분포의 시뮬레이션을 만들어 보았다. 이러한 방법으로 시뮬레이션을 만들면 전략개발의 테스트에 활용해 볼 수도 있다. 그러나 이 방법은 수많은 반복 횟수로 인해 시간이 많이 걸리기 때문에 그렇게 효과적이지는 않은 것 같다. 좀 더 효과적인 시뮬레이션을 위해서는 지수 분포에 대해 살펴볼 필요가 있다. 다음 시간에는 지수 분포의 특성과 시뮬레이션 방법에 대해 알아보기로 한다.

[출처]19. 호가창 포아송 분포의 시뮬레이션|작성자아마퀀트