News & Events
[알고리즘 트레이딩/전략편] 41. API로 Roll 모형의 Bid-Ask 스프레드 측정
- 2019년 1월 11일
- Posted by: 인사이트캠퍼스
- Category: 금융/AI/IT 기사

알고리즘 트레이딩 (Algorithmic Trading) – 전략 (41)
API로 Roll 모형의 Bid-Ask 스프레드 측정
호가창의 Bid-Ask 스프레드는 거래 비용과 밀접한 관계가 있다. 장 중에는 스프레드가 높을 때도 있고, 낮을 때도 있다. 변동성이 증가할 때는 시장 충격 계수가 증가하고, 유동성 척도는 낮아지고, 스프레드는 높아진다. (미시) 변동성, 유동성 척도 등은 주가뿐만 아니라 거래량도 관련되어 있으므로 독립적으로 측정하기가 어렵다. 반면에 스프레드는 독립적으로 비교적 쉽게 측정할 수 있다. 따라서 스프레드를 측정해 보면 변동성이나 유동성 등의 상황을 간접적으로 짐작해 볼 수 있다.
Bid-Ask 스프레드를 측정하는 방법으로는, 명목 스프레드 (Quoted Spread)와 유효 스프레드 (Effective Spread), 그리고 실질 스프레드 (Realized Spread)가 있다. 명목 스프레드는 호가창에 보이는데로 최우선 Ask 가격과 Bid 가격의 차이로 측정한다. 명목 스프레드는 대체적으로 장 중에 U-자형을 띤다. 장 초반과 후반에는 변동성이 높으므로 스프레드가 높게 측정되고, 장 중반에는 변동성이 낮아 스프레드도 낮게 측정된다. 따라서 명목 스프레드를 이용하면 특정 시점에 스프레드가 높은지 낮은지 확인하기 어렵다 (U-자형 패턴에 지배를 받으므로).

유효 스프레드는 최근 체결 가격 (Pt)과 호가창의 현재 Mid-price (Mt)를 이용해서 측정하고, 실질 스프레드는 최근 체결 가격과 가까운 미래의 Mid-price를 이용해서 사후적으로 측정한다. 유효 스프레드와 실질 스프레드는 모두 명목 스프레드에 비해 낮게 측정되며, 장 중에 U-자형 패턴이 나타나지 않는다. 따라서 유효/실질 스프레드는 장 중 특정 시점에 스프레드가 높은지 낮은지 판단하는데 유용하게 사용할 수 있다.
그런데 API를 이용하면 위의 스프레드를 거의 측정할 수 없다. API는 호가 틱의 상당 부분이 누락되므로, 현재 체결 가격과 동일한 시점의 Mid-price를 확인할 수 없다 (시차가 존재함). 체결 틱이 발생하면 호가 틱도 같이 변경될 것이므로 (잔량 등이 변경되므로) 변경된 호가 틱을 받아야 현재의 Mid-price를 알 수 있다. 변경된 호가가 들어오지 않는다면 과거의 Mid-price로 스프레드가 측정되기 때문에 측정값을 신뢰할 수 없다. 호가 틱의 누락이 없다는 가정 하에 실제로 측정해보면 스프레드 값이 매우 불안정하게 측정된다.
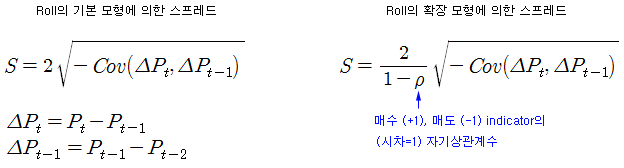
스프레드를 측정하는 좋은 방법으로는 1984년 Roll 이 제안한 모형이 있다. 위의 왼쪽 식은 Roll이 제안한 기본 모형이고, 오른쪽 식은 Roll의 기본 가정을 완화시켜 (매수, 매도 확률이 동일하다는 가정) 만든 확장 모형이다. 이 식은 스프레드를 측정하는데 아주 유용하게 사용될 수 있다. 그 이유는 호가 틱 없이 체결 틱만으로 Bid-Ask 스프레드를 측정할 수 있기 때문이다. Bid, Ask 호가도 필요 없고, Mid-price도 필요 없다. 체결 틱의 체결 가격만 있으면 된다. 따라서 이 모형을 이용하면 API에서도 장 중 Bid-Ask의 변화를 무리 없이 측정할 수 있다 (API에서 체결 틱은 거의 누락되지 않는다고 가정함).
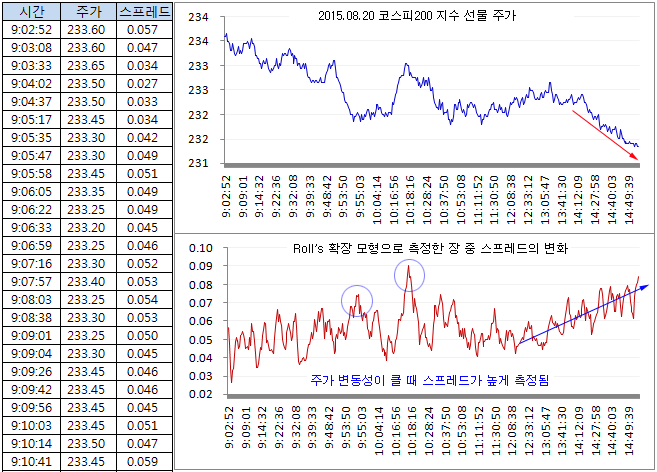
아래 그림은 2015년 08월 20일 코스피200 지수 선물의 체결 틱을 이용하여 Roll의 확장 모형으로 장 중 Bid-Ask 스프레드의 변화를 관찰한 결과이다. 장 중 스프레드는 최소 약 0.03부터 최대 0.09까지 움직이는 모습이다 (지수 선물의 Tick size는 0.05 임). 또한 명목 스프레드에 전형적으로 나타나는 U-자형 패턴은 보이지 않는다. 따라서 시간대 별로 스프레드의 특성을 파악할 수 있다. 예상대로 주가가 크게 변할 때 (변동성이 높을 때) 스프레드가 높게 측정되었다. 주가의 변동성과 관련된 특성으로 이전 시간에 살펴본 VPIN의 변화와는 또 다른 모습을 보여주고 있다.
그 동안 몇 편의 포스트를 통해 API를 활용해서 시장의 여러 특징을 관찰해 보았다. API가 호가 틱 데이터의 상당 부분이 누락된다는 큰 단점이 있긴 하지만, 시장미시구조론의 이론들을 활용하면 그런대로 유용한 분석을 할 수 있다 (DMA를 사용하지 않더라도).
이전 시간에 측정해본 호가창의 순 주문 흐름이나, 정보 비대칭 비용, VPIN 등과, 이번 시간에 살펴본 Bid-Ask 스프레드의 변화는 모두 가까운 미래의 주가와 (변동성과) 밀접한 관계가 있다. 미래의 주가를 예측한다는 것은 매우 어려운 일이다. 특히 어느 하나의 관측 사실로 미래의 주가를 판단한다는 것은 거의 불가하다. 여러 관측 사실들을 종합해서 하나의 신호로 만들면 상황이 좀 더 나아질 수 있을 것이다. 예를 들어 “정보 비대칭 비용이 낮은 상태에 있고, VPIN은 하락 추세에 있으며, Bid측과 Ask측 순 주문 유입량이 균형 상태에 있고, 스프레드도 낮은 상태를 유지하고 있다면 주가는 당분간 (ex : 십여 분 동안) 안정 상태를 유지하는 경향이 있다.” 라는 식의 결론을 도출해볼 수도 있다. 만약 이 결론이 타당하다면 이 기간 동안은 주가의 추세를 따라가는 전략보다는 마켓메이킹 같은 전략이 유용할 수 있다.
여러 관측 사실들로부터 종합적인 신호를 만들려면 기계학습 (Machine Learning) 같은 도구가 매우 유용하다. 기계학습은 관측된 여러 사실들을 학습하여 유용한 패턴을 검출하는데 뛰어난 능력을 가지고 있다. 이런 도구에 유용한 정보를 넣어줄 수만 있다면 분명히 유용한 결과가 나올 것이다. 물론 도구가 아무리 뛰어나더라도 유용하지 못한 정보를 넣어 준다면 결과도 유용하지 못할 것이다 (Garbage in garbage out).
참고로, 아래 내용은 XingAPI로 만든 XingScript 프로그램에서 Roll의 확장 모형을 이용하여 Bid-Ask 스프레드를 실시간으로 관찰하는 스크립트이다.
// Roll’s 확장 모형으로 Bid-Ask 스프레드를 실시간으로 측정한다.
// spread = 2 * sqrt(-Cov[dp(t), dp(t-1)]) : 기본 모형
// spread = 2 * sqrt(-Cov[dp(t), dp(t-1)]) / (1 – rho) : 주문의 연속성을 이용한 확장모형
// dp(t) : (t) 시점의 체결 가격 – (t-1) 시점의 체결 가격
// dp(t-1) : (t-1) 시점의 체결 가격 – (t-2) 시점의 체결 가격
// 스프레드는 K-기간 이동평균으로 측정함.
// ——————————————————————————————————
Set Queue xQ as Float // 가격 변화 dp(t) 저장용 Queue 설정 (실시간 이동 평균/공분산 계산시 필요함)
Set Queue yQ as Float // 가격 변화 dp(t-1) 저장용 Queue 설정
Set Array aPt[3] as Float // 체결 가격 저장용 배열. aPt[0] = p(t-2), aPt[1] = p(t-1), aPt[2] = p(t)
K = 300 // 300 체결 틱 이동 평균 스프레드 계산용
n = 0 // 전체 틱 수
cov = 0 // 초기 공분산
bt = 1 // 체결 틱의 초기 indicator (매수 주문 = +1, 매도 주문 = -1)
cont = 0 // 방향이 연속된 체결 틱 수
fd = OpenFile(“spread.csv”, “w”) // 결과가 저장될 파일을 오픈한다
// 처음에 체결 틱 3개를 받아서 체결 가격을 배열에 저장해 둔다. 초깃값.
For i=1 to 3
Wait(_ftick, _lob, 1) // 체결 틱이 발생할 때까지 대기한다.
aPt[0] = aPt[1]
aPt[1] = aPt[2]
aPt[2] = FilledInfo(_lob, _close) // 현재 체결 가격
Next
ax = aPt[2] – aPt[1] // dp(t)의 초기 평균
ay = aPt[1] – aPt[0] // dp(t-1)의 초기 평균
For loop = 1 to 2 step 0
Wait(_ftick, _lob, 1) // 체결 틱이 발생할 때까지 대기한다.
n = n + 1
// 스프레드 측정을 위해 체결 가격을 읽어오고, 최근 3-기간의 체결 가격을 기록해 둔다
price = FilledInfo(_lob, _close) // 현재 체결 가격
size = FilledInfo(_lob, _size) // 현재 체결 수량
aPt[0] = aPt[1]
aPt[1] = aPt[2]
aPt[2] = price
// 체결 수량으로 매수, 매도 indicator를 구분한다
If (size >= 0) Then
ct = 1
Else
ct = neg(1)
Endif
// 주문의 연속 확률로 indicator의 자기상관계수 (rho)를 계산한다. AR(1) 모형
If (bt == ct) Then
cont = cont + 1
Else Endif
rho = 2 * (cont / n) – 1 // 주문 indicator의 자기상관계수 (시차=1)
bt = ct
// Roll 확장 모형의 스프레드를 계산한다
// 1. dp(t) 과 dp(t-1)을 계산한다. x = dp(t), y = dp(t-1). 그리고 큐에 넣어둔다
x = aPt[2] – aPt[1] // dp(t) = p(t) – p(t-1)
y = aPt[1] – aPt[0] // dp(t-1) = p(t-1) – p(t-2)
r = Queue(_push, xQ, x)
r = Queue(_push, yQ, y)
// 2. x와 y의 실시간 이동 공분산 (Cov[])을 계산한다
If (n <= K) Then
// 실시간 공분산을 계산한다
cov = cov * (n – 1) / n + (x – ax) * (y – ay) * (n-1) / (n ^ 2)
Else
// 실시간 이동 공분산을 계산한다
xS = Queue(_pop, xQ)
yS = Queue(_pop, yQ)
cov = cov – (xS – ax)*(yS – ay)/K + (x – ax)*(y – ay)/K + (x – xS)*(y – yS)/(K ^ 2)
Endif
// 3. 다음 계산을 위해 실시간 이동 평균을 계산해 둔다
If (n <= K) Then
ax = ax + (x – ax) / n
ay = ay + (y – ay) / n
Else
ax = ax + (x – xS) / K
ay = ay + (y – yS) / K
Endif
// Roll’s 확장 모형으로 Bid-Ask 스프레드를 계산한다
If (neg(cov) >= 0) & (n >= K) Then
spread = 2 * sqrt(neg(cov)) / (1 – rho)
// 화면과 파일에 결과를 출력한다
Print GetTime(_krx, _time),” “, aPt[2], ” “, spread
Fprint fd, GetTime(_krx, _time),”,”, aPt[2], “,”, spread
Else Endif
Next
CloseFile(fd)
End

