[알고리즘 트레이딩/전략편] 21. VKOSPI 와 기초자산의 페어트레이딩

알고리즘 트레이딩 (Algorithmic Trading) – 전략 (21)

옵션의 변동성 전략 : Volatility Trading (4)

(VKOSPI 와 기초자산의 페어트레이딩)옵션 전략에서 변동성 (Volatility)의 의미는 대단히 크다. 오히려 주가지수 (S) 보다 더 큰 의미를 가질 수도 있다. 언제부턴지는 모르겠지만 변동성의 변화가 주가지수의 변화만큼이나 중요시되어 왔고, 앞으로는 변동성이 더 중요시되는 경향으로 흐르고 있다. 우리는 옵션을 처음 접할 때부터 기초자산 (S)이라는 시각에서 바라보고, 손익구조나 합성 포지션 등을 분석할 때도 대부분 기초자산의 시각으로 접근해 왔다. 그러나 이제는 변동성이라는 시각에서 접근하는 것이 더 합리적일 수도 있다.

어느 교재든지 옵션의 손익구조를 설명할 때, 아래의 왼쪽 그림과 같이 기초자산의 변화에 따른 옵션의 변화를 설명한다. 물론 이것은 정확히 맞는 설명이다. 만약 변동성 변화를 중심으로 콜옵션의 손익을 그려보면 어떻게 될까? 아마 맨 오른쪽 그림과 같이 될 것이다. 곡선의 형태가 그림과 같이 될지 반대의 곡률로 될지 분명치는 않지만, 변동성이 증가할수록 콜옵션의 가격은 하락하는 것으로 관측되고 있다. 이것은 이론적으로 설명하기 보다는 관측 사실로 설명이 된다. 이전 시간에 내재변동성이 증가할수록 기초자산의 가격이나, 콜옵션의 가격이 하락하는 것을 살펴보았었다. 참고로, 일반적으로는 변동성이 증가할 때 콜옵션의 손익은 증가하는 것으로 그려져 있다. 이것은 기초자산 가격이 일정하다고 가정한 경우의 변동성과 콜옵션 손익의 그래프이고, 기초자산 가격이 일정한 경우에는 정확히 맞는 설명이다 (베가를 설명하기 위한 그림). 그러나 현실적으로는 기초자산이 일정한 상태에서 변동성만 증가할 수는 없다. 따라서 변동성이 증가하면 콜옵션의 손익 그래프는 하락하는 것으로 그리는 것이 더 현실적이다.

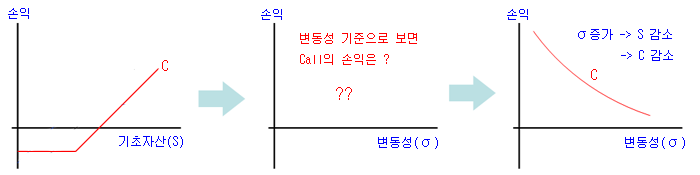
이처럼 변동성이 중시되는 시장에서는 기초자산이라는 시각에서 변동성이라는 시각으로의 전환이 필요해 보인다. Naked 포지션뿐만 아니라, 합성 포지션도 변동성의 관점에서 보면 다른 면모를 볼 수 있고, 어쩌면 의사결정의 결과까지도 달라질지 모른다.

이번에는 변동성과 관련된 합성포지션인 양매수나 양매도의 경우를 살펴보자. 아래의 왼쪽 그림은 기초자산의 관점에서 바라본 양매수 (C+P)의 손익구조이다. 델타-헤지 포지션으로 구성한 경우 기초자산이 많이 상승하거나 하락하면 수익이 발생하는 구조이다. 반면에 기초자산이 크게 상승하지 못하면 시간가치 하락만큼 손실이 발생하는 구조이다. 이 그림을 변동성의 시각으로 바라보면 오른쪽 그림과 같이 된다. 변동성이 증가하면 C+P는 수익이 발생하고, 변동성이 감소하면 시간가치만큼 손실이 발생하는 그림이 된다. 이 그림위에 -S나 -F를 그려보면 그림과 같이 될 것이다. 변동성이 증가할수록 기초자산의 가격은 하락하므로, 기초자산을 매도 (-S)하는 경우 수익이 발생하는 그림이다. 그러면 -S 와 C+P의 손익구조가 유사한 형태가 된다. 이 성질을 이용해 보면 S (F)와 C+P를 가지고 페어트레이딩을 고려해 볼 수도 있다. 단, S (F)와 C+P의 곡률이 달라 헤지 오류 (Hedge Error)가 발생하므로 단기간 거래에만 적용해 본다.

금융수학 편에서 변동성 지수 (VIX)를 설명할 때, Variance Swap에 대해 언급한 적이 있다. Variance Swap은 변동성 위험을 헤지하기 위한 장외파생 상품이다. Variance Swap은 VIX (VKOSPI)를 직접 매수 혹은 매도하는 상품으로 변동성 자체를 거래하는 것으로, 손익구조는 아래와 같다.

* Variance Swap 손익 = 변동성의 차이 [현재의 VKOSPI(Vi) – 만기시점에서 측정한 실제 변동성 (Vs)]

* (연속) 델타헤지 옵션 손익 = 시간가치 + 변동성의 차이

Variance Swap의 손익 구조는 위의 식과 같이 현재의 내재변동성 (VKOSPI, Vi라 하자)과 만기시점에 측정한 실제 기초자산의 변동성과 (Vs라 하자)의 차이가 된다. 매수자는 Vs가 Vi보다 큰 경우 수익이 발생한다. 따라서 미래의 변동성이 커질 것으로 예상되거나, 변동성이 커질 위험에 대비하기위해 Variance Swap을 매수한다. 한편, (연속) 델타헤지 옵션의 손익 구조는 시간가치와 변동성 차이의 합이 된다. 만약 연속 델타헤지 포지션에서 시간가치 부분만 없다면, 두 포지션은 동일한 것이 된다 (Variance Swap은 시간가치나 연속 델타헤지와 같이 지저분한 요소는 없고 깔끔하게 변동성의 차이로만 승부한다. 이 관계는 금융수학 편에서 수식으로 자세히 살펴볼 예정이다).

Variance Swap은 내재변동성 (VKOSPI)을 매수하거나 매도하는 것이고, 옵션으로 이것을 제대로 복제하려면 OTM/ATM의 콜/풋 옵션 전부를 이용하여 합성해야 한다. 그러나 이것은 가능하지 않으므로, VKOSPI를 대표할 수 있는 C와 P를 하나씩 선택하여 C+P로 델타헤지 포지션을 구성하여 Variance Swap의 대용치로 사용해 본다. 단, 시간가치와 연속 헤지 부분은 차이가 난다. 이 차이로 인해 위 그림에서 C+P와 S (F)의 곡률이 다르게 되고, 헤지 오류는 발생할 수 있다.

VKOSPI를 대표할 수 있는 C와 P의 선정이 문제가 될 수 있다. 보통의 경우 C의 내재변동성은 낮게 측정되고, P의 내재변동성은 높게 측정된다. 그리고 VKOSPI는 평균에 해당하므로, C와 P의 중간쯤에서 결정된다. 따라서 VKOSPI의 수준과 가장 유사한 수준의 C와 P를 선정해 본다.

만약 알고리즘 트레이딩으로 거래 시간이나 포지션 보유시간을 짧게 한다면, 시간가치의 변화와, 연속 델타헤지의 오류 부분이 줄어든다. 짧은 시간 동안의 시간가치 변화와 연속 델타헤지의 오류를 무시한다면, Variance Swap을 매수하는 것과 C+P를 매수하는 것이 비슷한 효과가 된다.

변동성 시각의 한 예로, VKOSPI와 기초자산에 대한 페어트레이딩 전략을 생각해 보자. 아래 그림처럼 VKOSPI와 기초자산을 페어로 스프레드를 계산해 본다. 스프레드는 페어트레이딩에서 다루었던 로그 스프레드로 하고, Cointegration Coefficient는 1로 한다. 그러면 스프레드는 그림과 같이 일정한 범위 안에서 진동할 것이다. 스프레드가 일정 범위를 벗어난 지점에서 진입과 청산을 고려해 본다. VKOSPI는 V로 표시하고, 기초자산 S대신 선물인 F로 페어트레이딩을 구성하는 것으로 한다. 스프레드가 일정한 범위에서 위로 벗어난다면 V와 F를 동시에 매도하고, 아래로 벗어난다면 V와 F를 동시에 매수한다. V를 매수하는 것은 C+P를 매수하는 것으로 하고, V를 매도하는 것은 C+P를 매도하는 것으로 한다.

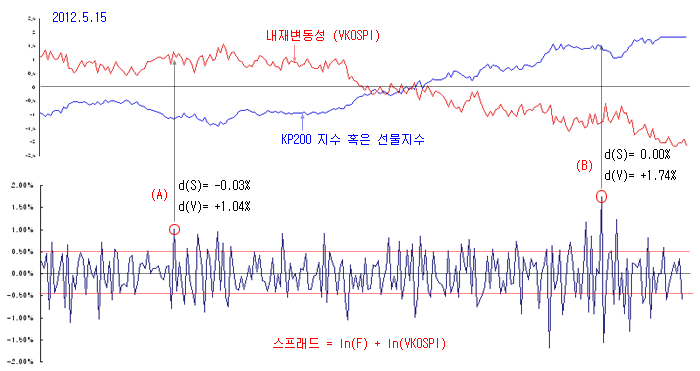
위 그림의 예에서, (A) 지점은 스프레드가 위로 벗어난 지점이므로, V와 F를 동시에 매도한다. (A) 지점은 S가 -0.03% 하락한 반면, V는 +1.04% 상승하였으므로, V가 하락하거나, S가 하락할 것으로 예상해 보는 것이다. 만약 S가 오르면 V는 더 많이 떨어질 것이기 때문에 페어트레이딩의 논리가 성립한다.

알고리즘 신호 (Signal) 생성 및 시나리오

1.OTM 및 ATM에 있는 콜옵션과 풋옵션을 이용하여 VKOSPI 지수를 실시간으로 계산한다. KRX에서 발표하는 30일 간의 변동성이 아닌 금융수학/변동성지수         (VIX)에서 살펴본 식으로 직접 계산한다.

2.실시간으로 계산한 VKOSPI와 유사한 수준의 콜옵션 (C)과 풋옵션 (P)을 선정한다.

3.VKSOPI와 선물가격의 스프레드를 계산한다. 스프레드 = ln(F) + ln(V)

4.스프레드의 실시간 평균을 계산하고, 일정범위의 상한선과 하한선을 결정한다.

5.스프레드가 상한선을 벗어나면 C+P와 F를 매도한다 (포지션 진입).

6.스프레드가 하한선을 벗어나면 C+P와 F를 매수한다 (포지션 청산).

위의 시나리오는 필자가 시험해 본 전략은 아니고, 이론적으로만 생각해 본 전략이다. 시간이 되면 간단히 프로그램을 만들어서 API로 시험해보고, 매매 성과를 포스팅해 보도록 하겠다.

참고로, 기초자산을 중심으로 생각할 때는 S = C – P 가 항상 성립하고, 합성선물 (F)을 구성할 때에는 F = C – P + K 와 같이 된다. 그리고 이 기준으로 Conversion이나, Reverse Conversion 같은 것을 고려하게 된다. 이 논리는 분명히 올바른 것이다. 다만, 알고리즘 트레이딩으로 매우 짧은 시간 동안의 거래에서는 S = C – P 보다 오히려 -S = C + P 가 더 합리적일 수 있다. 이것이 바로 변동성이라는 시각에서 바라보았을 때 의사결정의 결과가 달라질 수 있는 한 예가 된다.

[출처]21. VKOSPI 와 기초자산의 페어트레이딩|작성자아마퀀트