[금융수학] 35. 내재변동성 스마일 곡선 측정

금융 수학 (35)

내재변동성 스마일 곡선 측정

이번 시간에는 옵션의 시장가를 이용하여 기초자산의 내재변동성 스마일 곡선을 구하는 방법에 대해 알아본다. 옵션 시장에 참여한 거래자들이 결정한 가격에는 기초자산의 변동성이 내재되어 있다. 이것을 내재변동성 (Implied Volatility) 이라 한다.

블랙-숄즈 공식에 의하면 모든 행사가격의 옵션들은 동일한 변동성을 가져야 한다. 그러나 실제 시장에서는 행사가격 별로 내재된 변동성은 다르게 관찰된다. 이런 현상은 1987년 Wall Street crash 이후부터 나타나기 시작했다고 한다. 1987년 이전에는 행사가격 별로 내재변동성이 비교적 일정하였으나, 1987년 Crash를 경험한 투자자들은 기초자산 수익률 분포의 꼬리 부분이 정규분포보다 커질 가능성이 의외로 크다는 것을 알게 되었다  (Black Swan), 그 이후로는 OTM 영역의 내재변동성이 ATM 영역보다 크게 나타나기 시작했고, 행사가격에 따라 내재변동성이 곡선의 형태를 띠게 되었다 (내재변동성 스마일 곡선).

옵션의 시장가를 이용하여 내재변동성 스마일 곡선을 측정하려면 Call 옵션과 Put 옵션 가격을 모두 이용해야 한다. 그리고 ITM (In the Money) 영역의 옵션들은 Bid-Ask 스프레드가 넓고, 거래량과 유동성이 풍부하지 못하므로 시장 가격의 정보를 신뢰하기 어렵다. 따라서 ITM 영역의 가격들은 제외하고, 정보량이 풍부한 ATM ~ OTM 영역의 옵션 가격들만 이용한다 (VKOSPI 계산과 동일함). 그리고 옵션의 현재가는 Bid-Ask 스프레드의 영향을 받기 때문에 중간 가격 (Mid-price)을 이용한다 (스프레드가 충분히 tight 하다면 현재가를 그대로 이용해도 된다).

아래 결과는 2014.5.16.일 종가를 기준으로 내재변동성 스마일 곡선을 측정한 것이다. 내재변동성을 추정할 때는 기초자산 가격 (S), 이자율 (Rf), 잔존기간 (T-t) 등이 사용된다. 이자율이나 잔존기간은 충분히 알 수 있으나, 옵션 가격이 형성된 그 순간의 기초자산 가격 (S)은 정확히 측정할 수 없다 (거래소에서는 2초 마다 한번씩 S를 계산해서 통보해 준다). 따라서 S 도 추정해서 사용하는 것이 일반적이다. 아래 결과는 선물 가격 (F)으로 S를 추정해서 내재변동성을 측정한 결과이다. 옵션 가격이 형성된 순간의 F는 측정할 수 있고, F를 현재가치로 환산하면 S가 된다 (단, 베이시스 만큼의 차이는 존재함).

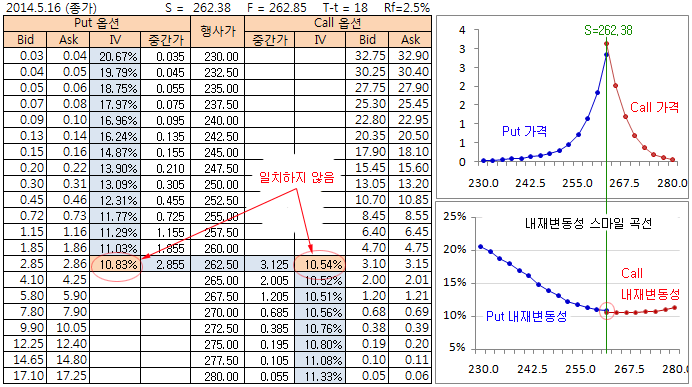
위 그림에서 F = 262.85 였고, 6월 만기이므로 해당 일수만큼 할인해서 S를 추정하면 S=262.38 이 된다. 추정된 S를 이용하여 각 행사가격 별로 내재변동성을 추정하면 된다. 그림처럼 Put 가격은 행사가격 230.0 ~ 262.5를 이용하였고, Call 가격은 행사가격 262.5 ~ 280.0을 이용하였다. 이 영역이 ATM ~ OTM 영역이다. 여기서 ATM은 S와 가장 가까운 가격으로 설정하였다.

이 방식으로 내재변동성 스마일 곡선을 측정하면 우측 하단의 그림과 같이 된다. 예상대로 스마일 모양이 나왔다. 그러나 한 가지 문제가 있어 보인다. Put 내재변동성과, Call 내재변동성이 연속되지 못하고 ATM에서 서로 다르게 측정된다 (Put 내재변동성이 약간 큼). 이것이 정상적일까? 정상적이지 않다. 이론적으로는 동일한 행사가격이라면 Put 내재변동성과 Call 내재변동성은 동일해야 한다. 그래야 풋-콜 페리티가 성립하고 차익거래 기회가 없는 균형상태가 된다.

이런 현상이 발생한 이유는 S를 추정할 때 F를 이용했기 때문이다. F는 S와 베이시스 만큼의 차이가 있기 때문에 (베이시스 차익거래 기회가 존재함. 컨버셜 or 리버셜) S의 추정치로 적합하지 못한 것 같다.

아래 경우는 옵션가격으로부터 S를 추정하여 내재변동성을 추정한 결과이다. 옵션 시장이 충분히 효율적이라면 차익거래 기회가 없을 것이므로, 옵션의 시장가격을 이용하여 S를 추정할 수 있다. 풋-콜 페리티 식을 이용하면 된다 (S = C – P + PV(K)). C와 P는 ATM 옵션의 가격을 이용하고, ATM은 C – P 가 최소가 되는 위치로 설정하였다 (ATM에서는 C 와 P가 동일해야 하므로 C – P가 최소가 된다).

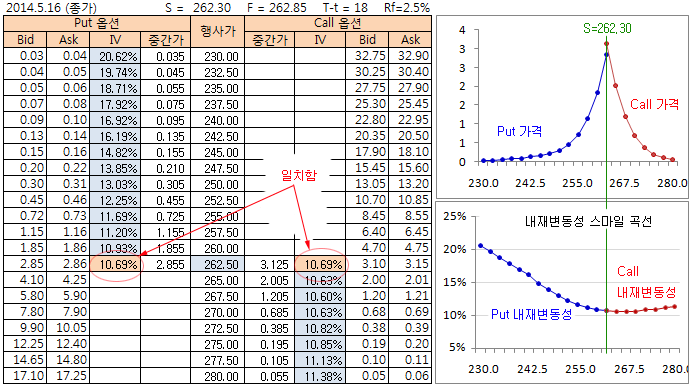
C – P가 최소가 되는 행사가격은 262.50 이고 Put의 중간 가격은 2.855, Call의 중간 가격은 3.125 이다. 이 가격으로 S를 추정하면 (S = 3.125 – 2.855 + 262.50 * exp(-0.025 * 18 / 252)), S=262.30이 된다. 이 S를 이용하여 내재변동성을 추정하면 위 그림과 같이 되고, ATM의 Put 내재변동성과 Call 내재변동성이 정확히 일치한다. 따라서 Call과 Put으로 측정된 내재변동성 스마일 곡선은 연속되게 그려진다 (우측 하단 그림). 스마일 모양으로 보면 S를 추정할 때 F를 이용하는 것 보다는 풋-콜 페리티를 이용하는 것이 더 의미가 있어 보인다.

이렇게 측정된 내재변동성 스마일 곡선으로부터 어떤 정보를 추출할 수 있을까? 스마일 곡선으로부터 만기 시점의 기초자산 (미래의) 확률분포를 추정할 수도 있고 (Risk Neutral Density : RND), 시간대 별로 스마일 곡선을 측정해서 관찰하면 곡선의 형태가 변화하는 것도 관찰할 수 있다. 곡선의 곡률이 좁아진다거나 넓어진다거나, 혹은 시계 방향이나 반시계 방향으로 회전한다거나 하는 변화를 관찰할 수 있고 (내재변동성의 Skew 현상), 이 변화로부터 현재 옵션 시장의 추가적인 정보를 더 많이 얻을 수 있다.

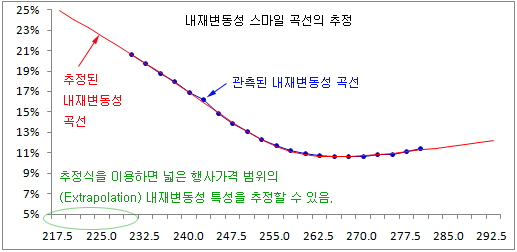
내재변동성 스마일 곡선의 변화를 체계적으로 관찰하려면 곡선의 함수식을 추정하는 것도 필요해 보인다. 위 그림은 관측된 내재변동성 곡선에 대한 추정 함수식을 만들어서 그려본 것이다. 파란색 점은 관측된 점들이고, 빨간색 선은 추정 함수식으로 그린 곡선이다. 추정 함수식이 점들에 잘 fitting 되어 있다. 함수식을 추정하면 함수에 포함된 여러 파라메터들의 변화를 읽어서 간접적으로 내재변동성의 변화를 쉽게 관찰할 수 있다. 이 부분에 대해서는 다음 시간에 자세히 알아보기로 한다.

[출처]35. 내재변동성 스마일 곡선 측정|작성자아마퀀트