[금융수학] 29. VIX (VKOSPI) 공식의 유도 과정

금융 수학 (29)

VIX (VKOSPI) 공식의 유도 과정

지난 두 편의 포스트에서 살펴본 로그 계약 (The Log Contract)과 일반화된 Pay Off 함수식을 이용하면 VIX 공식을 유도해 볼 수 있다. 유도 과정이 다소 복잡하긴 하지만, 무리한 가정이나 새로운 이론의 도입이 없어 비교적 순조롭게 진행할 수 있다.

아래 식 (1)과 (2)는 일반적인 기하브라운운동에 의한 주가의 모형이다. 금융수학의 앞부분에서는 이 식을 간단히 하기위해 Drift인 μ와 변동성인 σ를 상수로 취급하였지만 여기서는 변동성이 시간에 따라 변하는 모형을 다루어야 하기 때문에 Drift 만 일반 상수로 취급하고, 변동성은 시간에 따라 변하는 확률변수로 취급한다.

첫 번째 단계로 이모형에서 T 시점의 변동성을 추출해 낸다. 식 (2)의 양변에 로그를 취하면 식 (3)이 되고, 식(3)의 양변을 다시 미분하면 식 (4)가 된다. 식 (1)을 이용하여 dW를 제거하면 식 (5)가 된다. (위너 프로세스인 W는 수학적으로 처리하기 곤란하므로 제거할 수 있으면 제거한다)

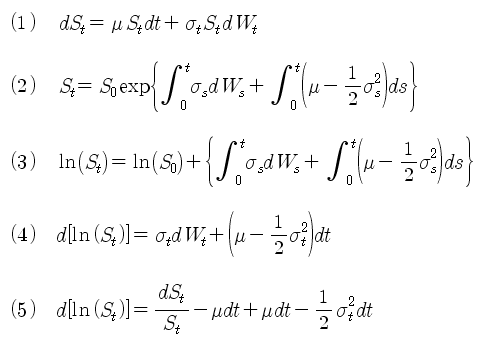
식 (5)를 정리하면 식 (6)이 되고, 식 (6)의 양변을 다시 적분하면 식 (7)과 (8)이 된다. 식 (8)의 양변을 T로 나누면 식 (9)가 되는데, 이 식이 바로 T 시점에서 측정한 변동성이 된다. 식 (9)의 좌변은 시점 0 부터 T 까지 변하는 변동성을 모두 적분하여 총 기간인 T로 나누어 주면 바로 T 시점에서 측정한 평균 변동성이 되는 것이다. 여기까지가 첫 번째 단계로 기하브라운 주가 모형에서 T 시점의 변동성을 추출한 과정이다.

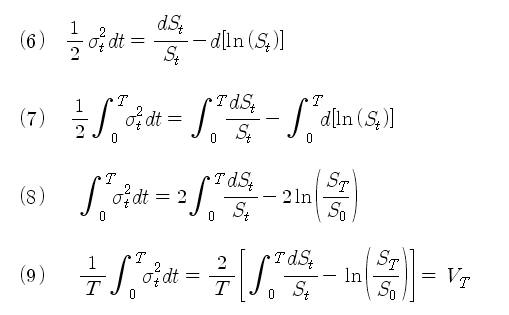
이제 이전 포스트에서 언급한 Variance Swap을 생각해 본다. T 시점의 기대 변동성이 바로 Variance Swap의 공정한 가치 (Fair Value)가 된다. 이것을 식으로 표현하면 식 (10)이 된다. 여기에 기하브라운 주가 모형에서 추출한 변동성을 대입하면, 식 (10)의 우변이 된다. 식 (10) 우변의 적분항은 0 ~ T 시점의 주가 수익률의 총 합이므로, T 시점의 최종 주가 수익률이 된다. 이것을 r 로 표시하면 식 (11)이 된다. 여기서 우리의 목적은 우변의 기댓값 E[.] 부분을 계산해 내는 것이다. 두 번째 단계에서는 이전 포스트에서 살펴본 로그 계약과 일반화된 Pay Off 함수식을 이용하여 이 기댓값을 계산해 내는데 초점을 둔다.

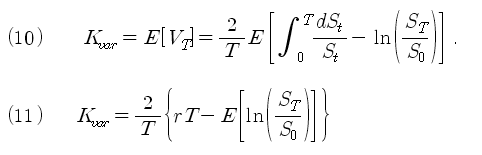
이제 두 번째 단계로 로그 계약 (The Log Contract) 모형에서 추출한 변동성을 이용해 본다. 로그 계약 포스트의 식 (12)에 있는 Pay Off가 바로 변동성의 표현이다. 이 식을 아래 식 (12)와 같이 쓰고, 1차, 2차 미분을 하면 식 (13)이 된다. 식 (14)는 지난 시간에 살펴본 일반화된 Pay Off 함수식이다. 식 (12)와 식(13)을 식 (14)에 대입하면 식 (15)가 된다. 여기서 S* 는 임의의 주가를 의미한다 (나중에 제거할 것임).

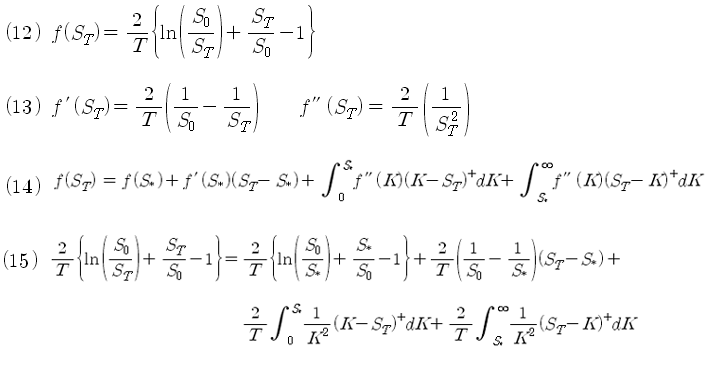
식 (15)를 정리하면 식 (16)을 얻을 수 있고, 양변에 기댓값을 취하면 식 (17)이 된다. 여기서 K, S* 는 모두 상수이고, T 시점의 주가인 ST 만 확률 변수이므로 식 (17)과 같이 쓸 수 있다. 식 (17)에서 E[(ST – K)+] 는 옵션의 만기 Pay Off의 기댓값이므로 옵션의 현재가치를 미래 시점인 T 시점의 가치로 환산하면 exp(rT) * C(K)가 된다. (단, C(K), P(K)는 현재 시점의 옵션의 시장가격임.)

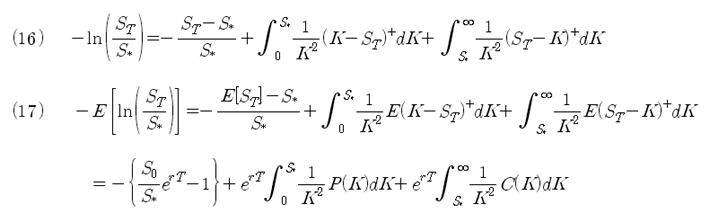
식 (18)은 일반적으로 성립하는 식이다. 식 (18)의 양변에 기댓값을 취하면 식 (19)가 된다. 식 (19)에 식 (17)을 대입하면 식 (20)을 얻을 수 있다. 이 식이 바로 위에서 목적했던 기댓값의 계산식이다. 식 (20)을 다시 위의 식 (11)에 대입하면 식 (21)을 얻을 수 있다.

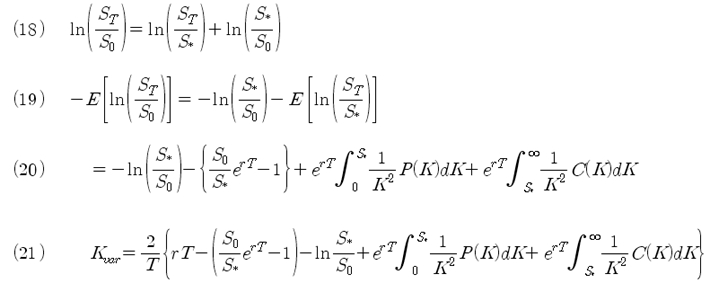
임의의 주가인 S* 를 식 (22)와 같이 선물 (선도)가격인 FT로 대치한다. 식 (22)을 식 (21)에 대입하면 식 (23)을 얻을 수 있다. 이 식이 바로 우리가 목표했던 Variance Swap의 공정가치인 변동성의 표현이고, VIX 에 대한 정의식이다.

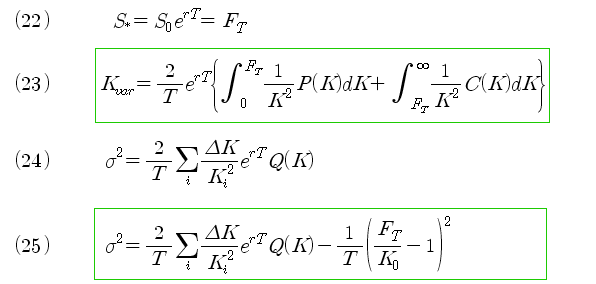
식 (23)은 VIX에 대한 연속 모형이고, 이 식을 이산 모형으로 변환하면 식 (24)가 된다. 여기서 Q(K)는, K가 (0 ~ FT) 까지는 풋옵션인 P(K)를 의미하고, (FT ~ 끝) 까지는 콜옵션인 C(K)를 의미하여, 식 (23)의 두 개의 적분항을 하나의 항으로 표현한 것이다. 그러나 식 (24)와 같이 이산 모형으로 쓰면 FT 지점에서 C(K)와 P(K)가 일치하지 않는 경우에는 약간의 오차가 발생한다. 이 오차를 보정해 주면 식 (25)가 되고, VIX의 최종식이 된다. 오차의 보정항에 대해서는 VKOSPI 계산의 질문에 대한 답변 포스트에 자세히 설명되어 있다.

[출처]29. VIX (VKOSPI) 공식의 유도 과정|작성자아마퀀트