[금융수학] 19. 옵션의 기대손익을 통한 이론가 계산

금융 수학 (19)

옵션의 기대손익을 통한 이론가 계산

콜옵션을 1계약 매입하면 기대할 수 있는 기대수익은 얼마가 될까?

만기 시 기대수익을 현재가치로 환산한 것이 계약 당시 지불한 콜옵션의 프리미엄과 정확히 일치하고, 이 프리미엄이 콜옵션의 가격이 된다. 따라서 현재 콜옵션의 가격이 향후 기대할 수 있는 기대수익이 되는 것이다. 사실 블랙숄즈 옵션가격 공식을 유도할 때 이미 이 관계가 이용되었다. (블랙숄즈 옵션공식의 유도과정 식 (1) 참조). 이번 시간에는 실제로 기대수익을 계산해 보고, 이 값이 옵션의 이론가와 정확히 일치하는지 확인해 보도록 한다.

아래의 왼쪽 그림은 콜옵션의 만기손익과 기하브라운운동 (Geometric Brownian Motion)에 의한 기초자산의 가격분포를 그린 것이다. 만기 시 기초자산의 가격 (S)은 기하브라운운동에 의해 평균과, 분산의 특징에 따라 아래 그림과 같이 분포하고, 분포함수 (PDF)는 로그정규분포를 따르는 f(S)로 나타낼 수 있다. 기초자산의 가격이 옵션의 행사가격보다 크면 매입한 옵션이 행사가능한 상태가 되고, 행사확률은 블랙숄즈 공식의 N[d2]가 된다 (옵션의 행사확률 공식 유도 참조).

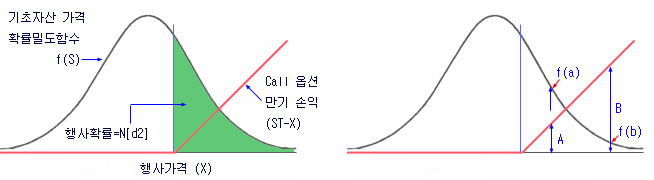
오른쪽 그림은 만기 시 가능한 손익과 확률을 그려본 것이다. 만기 시 수익 (ST-X)이 A가 되는 확률은 f(a)이고, 수익이 B가 되는 확률은 f(b)이다. 수익 (A)이 작으면 확률이 커지고, 수익 (B)이 커지면 확률이 작아진다. 만기 시 콜옵션 수익의 상한선은 무한대라고 하지만 확률은 거의 0에 가깝게 된다.

만기 시 기대할 수 있는 기대수익을 구하려면 수익*확률 값을 전부 더해주면 된다. 즉, (ST-X) * f(S)를 전 구간에 대해 적분해 주면 된다. 이 관계를 나타낸 것이 아래의 식 (2)이다. 기대수익은 만기 시의 가치이므로, 현재가치로 환산하면 식 (3)과 같이 되고, 이 값이 바로 현재 콜옵션의 프리미엄인 이론적 가치가 된다.

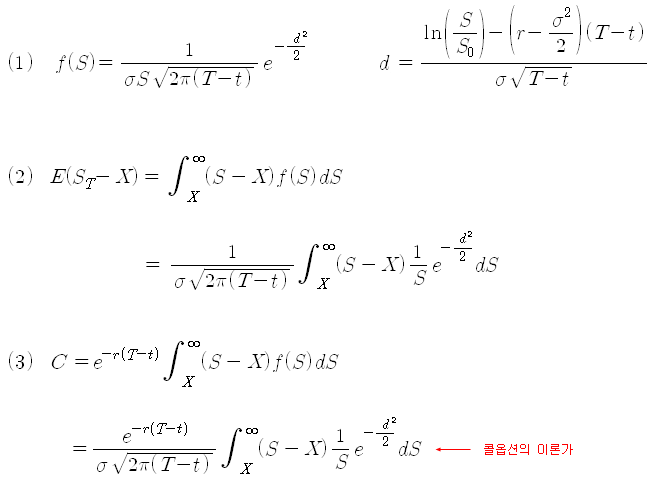
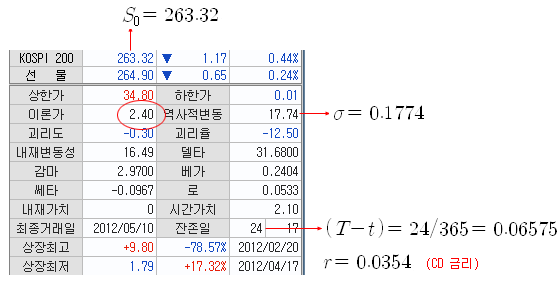
위의 관계식을 이용하여 콜옵션의 이론가를 실제로 계산해 보고, 블랙숄즈로 계산한 값과 일치하는지 확인해 보자. 아래 그림은 2012.4.17 현재 (종가 기준), 키움증권의 HTS에서 확인한 행사가격 X=270.0 에 대한 기본 자료이다. 기초자산인 KOSPI200의 가격 (S0)은 263.32이고, 역사적변동성는 0.1774, 잔존기간은 24일이고, 무위험 이자율은 CD 금리를 적용하였다. HTS상의 이론가는 2.40이고, 이 값은 블랙숄즈 공식에 의해 계산된 값이다.

이 데이터를 이용하여 만기 시 기대손익을 계산하여 옵션의 이론가를 계산해 보자. 아래의 식은 계산 과정을 나타낸 것이다. 식이 복잡하므로 식 (4)에서 기본적인 항목들을 미리 계산해 놓았다. 식 (4)의 결과를 식 (3)에 대입하면, 식 (5)와 같이 된다. 식 (5)의 적분값 계산은 온라인 적분계산기를 이용하였다 (주-1 참조). 계산 결과는 위의 이론가 2.40과 정확히 일치한다. 블랙숄즈 공식으로 계산한 이론가와, 만기 시 기대수익을 통해 계산한 이론가가 정확히 일치하고 있다.

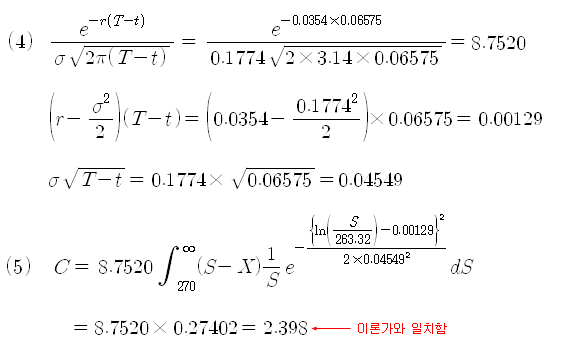
사실 이 결론은 당연한 결과이다. 블랙숄즈 옵션공식은 이미 이 과정을 통해 계산된 것으로, 이 과정을 일반화 시킨 것이기 때문이다. 합성옵션의 경우도 마찬가지이다. 만약 C1-C2로 Bull Spread 합성 포지션을 구축했다면, 만기 시 기대할 수 있는 기대수익은 C1-C2가 된다.

주-1) 온라인 적분 계산기

URL : http://www.solvemymath.com/online_math_calculator/calculus/definite_integral/index.php

[출처]19. 옵션의 기대손익을 통한 이론가 계산|작성자아마퀀트