[금융수학] 9. 금융수학 – 옵션의 행사확률 공식 유도

금융 수학 (9)

옵션의 행사확률 공식 유도

이전 포스트의 기하 브라운 운동으로 만든 주가 모형을 이용하면, 만기 시 옵션이 행사될 확률을 계산해 볼 수 있다. 계산 결과는 흥미롭게도 블랙-숄즈 공식의 N[d2] 와 일치한다. 사실, 이 계산을 통해 N[d2]가 옵션의 행사 확률이라는 것을 알 수 있는 것이다. 여기서는 행사 확률을 구하는 공식을 유도해 보고, 몬테카를로 시뮬레이션으로 공식이 잘 만들어졌는지 확인해 보도록 하겠다.

주가의 흐름이 랜덤 워크 과정임을 가정하면, 주가는 현재 시점 (t)에서 출발하여 옵션의 만기 시점 (T) 까지 아래 그림과 같이 예측할 수 없는 경로를 따라 움직인다. 만기 시점의 주가는 그림과 같이 확률분포를 형성하며, 행사가격이 X인 옵션이 만기 시점 (T)에서 행사 가능하려면 ST > X 가 되어야 한다. 이 때 만기 시 주가 ST 가 X 보다 큰 확률인 P(ST > X)를 구하면, 이것이 행사 확률이 된다.

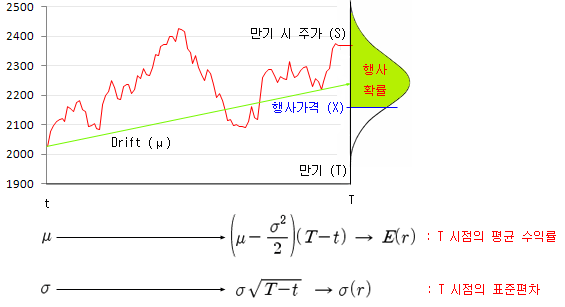
이전 포스트에서 살펴 본 바와 같이, 현재 시점 (t)에서 측정된 주가의 일일 평균 수익률 (u)이 만기 시점에서는 평균 기대 수익률인 E(r)로 예측되고, t 시점의 표준편차는, 만기시점에서는 시그마(r)로 분포된다. 만기 시점의 주가의 확률분포는 정규분포이고, 평균과 표준편차는 E(r)과 시그마(r)이 된다. 이제 P(ST > X) 를 구하기 위해 ST > X를 아래 수식과 같이 변형한다.

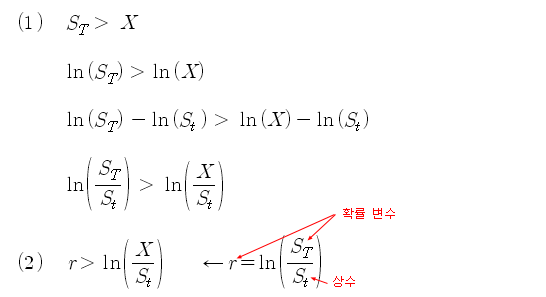
식 (2)에서 r은 t ~ T 기간 동안의 수익률이며, St는 현재의 주가이므로 알려진 값이지만, ST는 T 시점의 주가이므로 확률변수가 된다. 따라서 r도 확률변수가 되고 정규분포를 이룬다. 식 (2)를 평균인 E(r)과 시그마(r)을 이용하여 표준정규분포 (Standard Normal Distribution)로 변환하면 아래와 같이 된다.

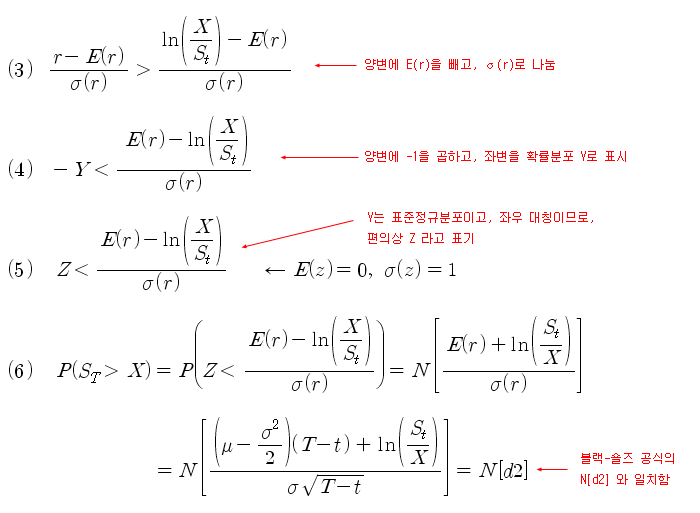
식 (6)의 최종 결과는 흥미롭게도 블랙-숄즈 공식의 N[d2]와 일치한다. 이 식의 계산값이 행사 확률을 잘 나타낼 수 있는지,  몬테카를로 시뮬레이션을 통해 확인해 보자. 아래의 엑셀 화면은 이전 포스트에서 사용한 파일에, 행사가격, 잔존기간, d2, N[2]를 추가하여 식 (6)을 계산해 보고, 몬테카를로 시뮬레이션을 4,000 회 수행하여 만기 시 주가가 행사가격보다 큰 경우의 수를 구해서 그 비율을 계산해 본 것이다. 잔존기간은 100일로 하고 행사가격은 2,080으로 가정하였다 (코스피200이 아니라 코스피에 대한 옵션으로 가정). 결과는 아래 그림의 빨간색 원 부분인 N[d2] 와 시뮬레이션으로, 두 결과가 거의 일치하고 있다. 따라서 식 (6)으로 만든  행사확률 공식은 잘 만들어졌다고 볼 수 있다.

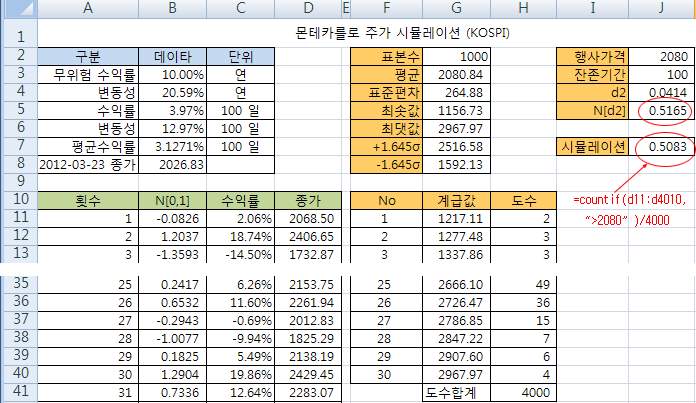
그러면 아래의 블랙-숄즈 옵션 공식에서 N[d2]의 실체가 행사확률로 밝혀진 것이다. 참고로 N[d1]은 앞으로 밝히겠지만, 주가 (S)에 대한 헤지 비율 혹은 주가 (S)에 대한 옵션가격 (C)의 변화율인 델타 값이다.

이번 포스트에서는 옵션의 행사확률 공식을 유도해 보았다. 실무적인 책자나 자료에서는 N[d1]을 행사확률이라고 설명한 것들이 많다. 이것은 주가가 오르면 N[d1]이 증가하고, N[d2]도 같이 증가하므로, N[d1]이 높아지면 행사확률도 높아지기 때문에 편리상 N[d1]을 행사확률의 대용치로 사용하고 있는 것이다 (반대로 N[d1]이 낮아지면 행사확률도 낮아진다). 행사확률이 70% 라든지, 73% 라든지, 숫자의 크기가 중요한 것이 아니라 확률이 높아지는지, 낮아지는지가 중요할 수도 있기 때문에 큰 무리는 없어 보인다.

[출처]9. 금융수학 – 옵션의 행사확률 공식 유도|작성자아마퀀트