News & Events
[금융수학] 5. 블랙 숄즈 옵션 공식 유도 (4) -편미분 방정식 풀기 (PDE 3/3)
금융 수학 (5)
블랙 숄즈 옵션 공식 유도 (4) -편미분 방정식 풀기
(PDE 3/3)이전 포스트에서 구한 열 확산 방정식의 해인 아래 1) 식에서부터 블랙 숄즈 옵션 공식을 완성해 보자. 식 1)의 경계조건은 이전 포스트의 식 10) 으로부터 나온 것이며, y(u, x)에서 u = a 이고, 옵션 만기인 x = 0 (잔존기간=0) 일 때의 조건이다.
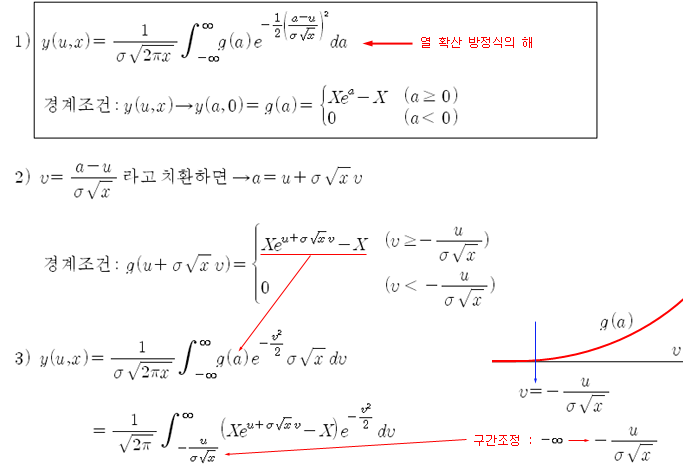
식 2)와 같이 변수를 치환하면 경계조건이 식 2)의 두 번째 식으로 변환되고, 식 1)은 식 3)으로 변환 되고, 적분 구간도 변환 된다. 식 3)을 두 부분으로 나누면 식 4)가 되고, 첫 번째 항 (A) 와 두 번째 항 (B)를 각각 다시 계산한다.
각각 계산한 (A)와 (B)를 다시 식 4)에 대입하면 최종적으로 식 5)를 얻을 수 있다. 이 식을 자세히 들여다보면 표준정규분포의 확률밀도함수 (PDF)가 된다. 아래 그림은 표준정규분포 함수의 그래프이며, 정규분포 곡선의 면적이 누적확률밀도함수 (CDF)가 된다. 따라서 식 5)는 정규분포를 의미하는 N[] 표기로 바꾸어 쓸 수 있다.
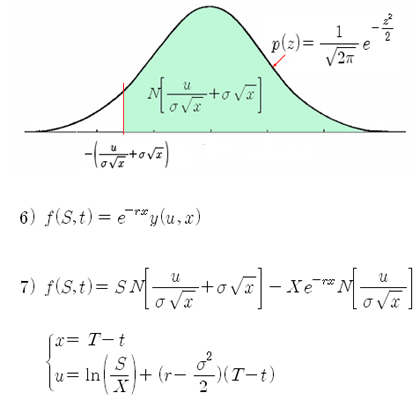
우리가 최종적으로 얻고자 하는 해는 f(S,t) 이므로 식 5)를 식 6)에 대입하면 최종 해를 구할 수 있다. 식 7)이 바로 우리가 여태껏 얻고자 했던 블랙 숄즈 편미분 방정식의 최종 해이다. 정말 군더더기 하나 없는 깔끔한 식이 되었다 (여기서 블랙과 숄즈는 어떤 기분이 들었을까? 정말 대단한 풀이 과정이 아닐 수 없다).
f(S,t)가 우리가 목표했던 옵션의 현재가치 이며, 일반적으로는 아래와 같이 표현한다.
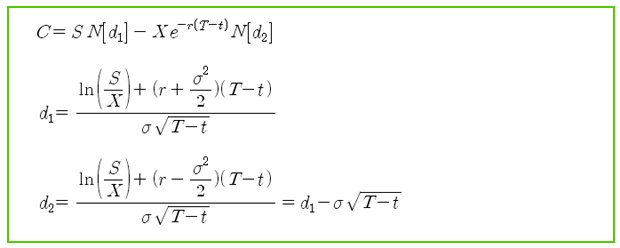
이 식은 금융의 전 분야에 걸쳐 아주 많이 사용된다. 이 식으로 인해 잔존 기간에 따른 옵션의 이론가를 계산할 수 있을 뿐만 아니라, 각종 옵션의 민감도를 계산할 수 있다. 단순히 이론가나 민감도 계산에 그치는 것이 아니라 기존의 재무관리 전 영역에 걸쳐 대단히 큰 영향을 끼치고 있다.
무려 4편의 포스트를 통해 블랙 숄즈의 옵션 공식을 고전적인 방법으로 유도해 보았다. 첫 포스트부터 무거운 주제를 다루게 되었지만, 이후 포스트부터는 Stochastic Calculus를 통해 금융수학의 내용들을 다루어야 하므로, 고전적인 방법에 대해 언급할 기회가 없을 것 같아 첫 부분에 PDE를 언급하게 되었다. 다음 시간부터는 Stochastic Calculus를 통해 이 공식의 각 부분들에 대해 자세히 분석해 보고, 활용하는 방법 등에 대해 알아보도록 한다.
유도 과정이 상당히 복잡했지만, 간단히 요약해 보면 다음과 같다.
1 단계 : 편미분 방정식 만들기
2 단계 : 물리학의 열 확산 방정식으로 변환하기
3 단계 : 열 확산 방정식의 해 구하기
4 단계 : 열 확산 방정식의 해를 변형하여 옵션가격 공식 만들기
참고자료 : 블랙 숄즈의 편미분 방정식 (1999. Ishimura Sadao & Sonolsu)
공업수학 (Kreyszig)
