News & Events
[Machine Learning] 23. 뇌신경망을 이용한 머신러닝 (Neural Networks) 구현하기
- 2019년 1월 14일
- Posted by: 인사이트캠퍼스
- Category: 금융/AI/IT 기사

여기까지 여러분은 NN에 대한 모든 기본 개념을 배웠습니다.
이제 구현을 하기 위해서 몇가지 더 알아야 할 것들을 배우고 실제로 구현이 어떻게 되는지를 살펴보도록 하겠습니다.
Unrolling Parameters
아래 그림에서와 같이 Octave로 실제 구현을 할때 사용되는 values에 대해서 알아보겠습니다.
costFunction의 입력 값이 되는 theta와 Advanced Optimization Algorithm을 사용할때 입력 값이 되는 initialTheta는 각 layer별로 theta들이 있기 때문에 Matrix가 되어야 하는데, 이것을 하나의 Vector로 만들면 좋습니다. 계산하고 사용하기가 편리하겠죠. 이것을 하는 방법이 Unrolling 입니다.
마찬가지로 costFunction의 계산된 결과 중에 하나인 gradient도 n+1의 크기를 갖는 Vector로 처리하게 됩니다.
그리고 L=4 즉, Layer가 4개로 구성이 되어 있는 NN에서는 theta가 3개의 vector로서 존재하고 우리가 원하는 최종적인 parameter(D)도 3개가 될 것입니다.

각 layer별로 units이 10개, 10개로 구성된 hidden layer 2개와 1개의 output으로 구성된 NN을 예제로 살펴보겠습니다.
이때 세타(1)은 10 x 11 크기를 갖는 Matrix가 됩니다. 연결된 선들을 잘 살펴보시면 그 이후를 알 수 있을 것입니다. 역시 세타(2)도 동일한 크기를 가지겠죠. 그리고 세타(3)은 1 x 11의 크기를 갖는 Vector가 됩니다.
마찬가지로 D 크기도 동일하게 됩니다.
3개의 Theta들을 쭈욱 펼쳐서(Unrolling) 하나의 Vector로 형태를 변경하고 이를 thetaVec 이라는 이름으로 만들기 위해서는 아래 그림의 중앙부분의 명령어를 실행하면 됩니다. 그리고 바로 밑에 D에 대한 펼쳐진 Vector를 DVec 이라고 만들었습니다. Octave에서 임의의 Matrix를 만들어서 실행해보시면 바로 감이 오실 것입니다.
그리고 이렇게 하나로 합쳐진 thetaVec은 reshape라는 명령어를 사용해서 다시 나눌 수 있습니다. 아래 그림 하단에서와 같이 n+1의 크리로 다시 분리하여 각각의 theta로 나누는 것을 볼 수 있습니다.

이 방법을 이용해서 알고리즘이 수행되는 과정을 정리하면 다음 그림과 같습니다.
초기 parameters인 세타1,2,3을 unroll하여 하나의 Vector인 initialTheta를 생성하고 이것을 입력값으로 하여 fminunc 알고리즘을 수행하게 됩니다.
알고리즘이 수행되면서 내부적으로 실행하는 costFunction에서는 입력 받은 thetaVec을 다시 theta1,2,3으로 분리하여 연산할때 사용하고 그 결과로 리턴되는 D1,2,3을 다시 unroll하여 gradientVec으로 최종 결과를 리턴해주면 되겠습니다.

Gradient Checking
Back Propagation 은 실제적으로 상당히 민감하여 작은 버그에도 손상이 커질 수 있는 특징이 있습니다. 구현해서 실행을 시켜보면 J함수의 cost가 줄어드는 것처럼 보이더라도 실제로는 충분히 감소가 되지 않아 성능을 떨어뜨리거나 문제가 발생 할 수 있습니다.
이것을 해결하기 위해서 체크하는 로직이 필요한데 이것을 Gradient Checking이라고 합니다.
개념은 아래 그림과 같습니다.
우리의 J 함수가 있으면 이것을 미분하여 기울기(파란색 직선)를 따라 알고리즘이 하강하는 것이였습니다. 이와 비슷하게 미분을 하지 않고 수치적으로 기울기를 만들어 낼 수 있습니다. 세타를 기준으로 Epsilon 이라고 정의된 수치만큼 더하고 빼서 그 사이의 J값을 직선으로 연결하면 빨간색 선과 같이 본래의 것과 비슷한 기울기를 가지는 직선을 만들어 낼 수 있다는 것입니다.
그리하여 J 함수를 세타로 편미분한 값은 ( J(세타+E) – J(세타-E) ) / 2E 와 비슷한 값을 나타내며 이때 Epsilon의 값은 아주 작은 0.0001 정도의 값이 됩니다. 너무 사이가 벌어지면 기울기와 전혀 다른 값이 되므로 아주 작게 만들어줍니다. 그리고 이것을 꼼수를 쓴다고 오른쪽 엑스 표시의 공식과 같이 한쪽만 적용하는 것은 전혀 다른 값이 되어 좋치 않습니다.
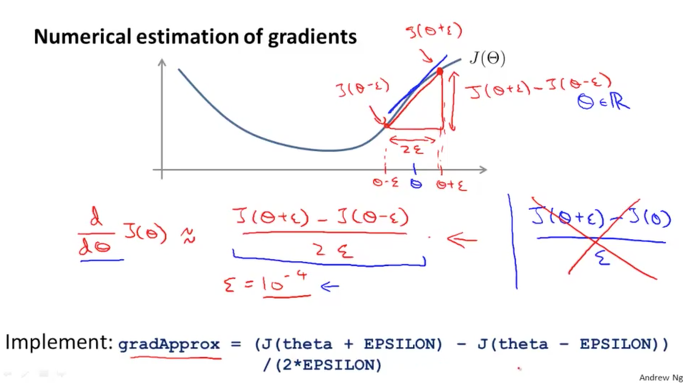
위의 개념을 이용해서 Parameter 세타를 편미분하여 계산할때 아래 그림과 같이 편미분의 대상이 되는 세타에 +E, -E를 해주고 2E로 나누어주어 구현을 하면 됩니다.

이를 Octave에서 구현하면 아래와 같이 반복문과 명령문으로 연산이 됩니다. 그리고 최종적으로 gradApprox의 값과 DVec의 값을 비교해서 비슷하다면 정상적으로 NN이 동작하고 있다는 것입니다. 만약 값이 다르다면 어딘가 문제가 있는 것이니 확인을 해야 할 것입니다.

지금까지 내용을 정리하면 아래 그림과 같습니다.
DVec을 Back Propagation 알고리즘으로 계산을 하고, 체크를 위해서 만든 gradApprox를 계산을 해서 두개의 값을 비교했을때 비슷한 값이면 오케이입니다.
그렇게 문제가 없음을 확인한 다음에는 실제 학습을 위해서 BP를 실행하기 전에 반듯이 이 numerical gradient check를 비활성화 시키도록 해야 합니다.
이것은 반복문을 사용해서 매 턴마다 수치적인 계산을 하고 있기 때문에 활성화가 되어 있으면 상당히 느리게 동작이 될 것이기 때문입니다.

Random Initialization
이번에는 초기 parameters를 셋팅하는 것에 대해서 알아보겠습니다.
Gradient Descent 혹은 Advanced Optimization을 사용함에 있어서 초기 parameter(세타) 값을 설정하여야 했습니다.
기존에는 0의 값으로 셋팅을 했었는데 NN에서도 0의 값으로 셋팅을 해도 되는 걸까요?

모든 parameters를 0의 값으로 셋팅을 했다고 가정을 해보겠습니다.
아래 그림과 같이 input values는 연결된 라인을 따라서 weight와 연산이 되면서 진행이 되는데 이때 값이 0이기에 결과도 0이 되는 것은 아니지만 모두 같은 연산을 수행하게 되는 것을 이해할 수 있습니다. (이전에 AND, OR연산 하는 부분을 보시면 감이 오실 거라고 생각이 됩니다.) 동일한 weight로 동일한 연산이 모든 unit에서 발생하므로 아래 공식들과 같이 값은 값이 만들어집니다.
그것은 결국 NN을 사용하는 benefit이 없어지는 것이 됩니다.
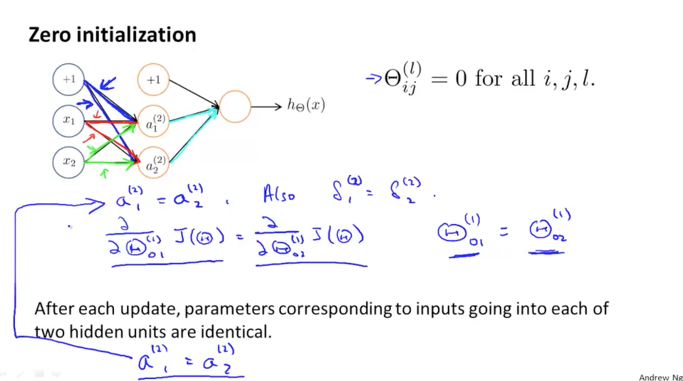
그럼 어떻게 하는 것이 좋을까요? 랜덤하게 초기화를 시켜주는 것입니다.
이것을 Symmetry breaking이라고 표현을 했는데 대칭이 되는 것을 피하는 방법이 되겠습니다.
그러므로 각각의 parameter인 세타의 값에 랜덤하게 차등을 줌으로서 이를 해결할 수 있습니다. 이 차이는 작은 값의 Epsilon의 양수와 음수 사이의 값을 갖도록 해주기 위해서 더하고 빼고 하여 생성합니다.
아래 예제로 Theta1 을 Octave에서 구현할때 명령문을 보시면 이해가 되실 것이라고 생각합니다.
Theta1의 rand 함수는 10 x 11의 크기를 갖고 각각의 값들은 0~1 사이의 값이 됩니다. 여기에 2배의 Epsilon을 곱하고 다시 1배의 Epsilon을 빼서 생성을 한 모습입니다.

추가적으로, Epsilon의 초기값을 셋팅하는 방법은 루트6 나누기 루트( in Layer의 units수 + out Layer의 units수 + 1(bias) ) 으로 구할 수 있습니다.

