[페어 트레이딩/기초편] 19. 분할 페어트레이딩

페어트레이딩 (Pairs Trading) – 기초(19)

분할 페어트레이딩   

페어트레이딩을 할 때 포지션은 분할로 진입하는 것이 유리하다. 그 이유는 스프레드의 최저점에서 진입하기가 매우 어려우므로 평균적인 저점에서 진입하는 것이 위험을 줄이는 한 방편이 되기 때문이다. 또한, 분할로 진입하면 스프레드의 단기 변동성이 줄어들어 심리적으로도 도움이 된다. 일반 방향성 투자의 경우도 마찬가지일 것이다.

단기적인 방향성 투자는 투자에 성공할 확률이 그리 높지는 않는 것 같다. 투자 의사결정의 가장 중요한 요인은 종목 선정과 매매 타이밍일 것이다. 만약 투자자가 종목 선정에 성공할 확률이 80% 라고 가정하고, 매매 타이밍을 맞출 확률도 80% 라고 가정해 보자 (80%면 꽤 높은 편이다). 그러나 최종적으로 투자에 성공하려면 두 요인이 동시에 만족되어야 하므로, 최종 확률은 64%가 된다 (80% x 80%). (지나친 비약일지 모르겠지만) 이렇게 성공 확률이 낮아지기 때문에, 의사결정이 잘못된 경우 손절(Loss Cut)로 위험을 줄이게 되지만, 빈번한 손절은 최종 수익률에 큰 영향을 미치게 된다.

페어트레이딩의 경우에는 시장중립전략인 롱/숏으로 이미 위험을 줄인 상태이기 때문에, 빈번한 손절은 바람직하지 않다. 해당 페어의 Cointegration 관계를 확인하고 스프레드의 특성을 확인해서 내린 의사결정이라면, 단기적으로는 손실이 나더라도 충분히 기다려 볼 만하다. 빈번한 손절보다는 분할로 진입하는 것이 유리하다.

그럼 분할 진입의 효과를 예를 통해 살펴보자 (삼성물산과 CJ CGV 페어). [그림-1]의 아래쪽 차트는 삼성물산의 600일 간의 주가 차트와 삼성물산의 10일 이동평균선이다. 위의 차트는 삼성물산의 주가 차트와 이동평균 사이의 스프레드 차트이다. 그림에서 알 수 있듯이 스프레드가 매우 안정이고 거의 완벽한 수준의 Cointegration 관계를 보인다.

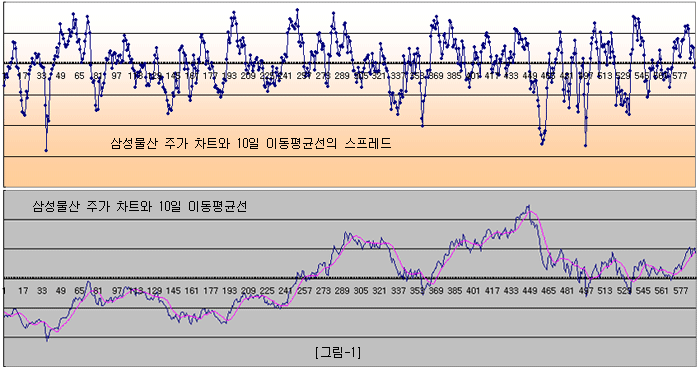
만약 위의 스프레드에 투자가 가능하다면 큰돈을 벌 수 있을 것이다. 그러나 동일 상품의 이동평균을 복제할 방법이 없으므로 이 스프레드에 투자할 수는 없다. 삼성물산이라는 동일 상품에 대해서 주가와 이동평균을 페어로 구성할 수가 없는 것이다.

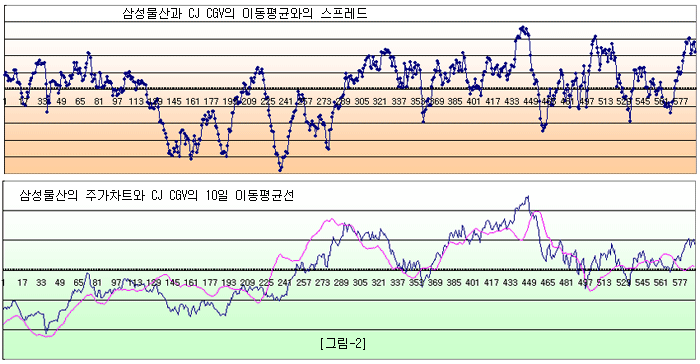
그림-1]에서 삼성물산의 이동평균 대신 페어 측인 CJ CGV의 이동평균을 대입해 보면 [그림-2]와 같이 된다. [그림-1] 보다 스프레드의 정상성은 떨어지지만, 페어가 Cointegration 관계에 있으므로 이동평균 기간이 늘어날수록 [그림-1]에 가까워 질 것이다. 이동평균에 투자한다는 것은 분할 매수를 의미한다. 예를 들어 10일간 분할로 매수한다면 평균 매수가격은 10일 이동평균이 된다. 그러나 이 경우도 동일한 상품은 아니지만 시점이 다르기 때문에 페어로 묶을 수 없다.

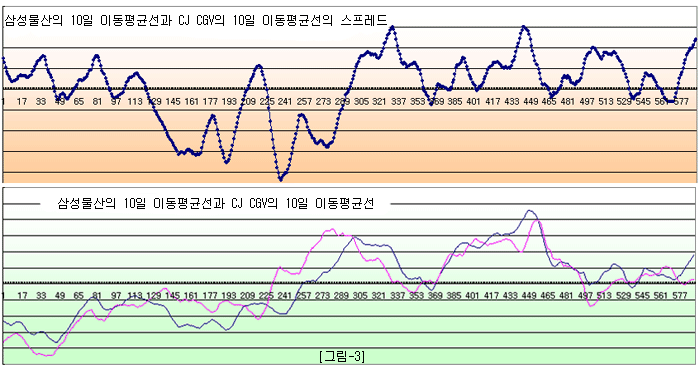
[그림-3]은 서로의 이동평균을 페어로 묶은 것이다. 이 경우는 투자 시점이 일치하고 상품이 서로 다르기 때문에 페어트레이딩이 가능하다. 즉, 삼성물산과 CJ CGV를 분할로 진입하면 된다. 그러면 스프레드는 단기 변동성이 줄어들고 굴곡이 완만해 진다. [그림-3]의 스프레드는 결국 삼성물산과 CJ CGV 페어의 원래 스프레드에 이동평균을 취한 것과 일치 할 것이다.

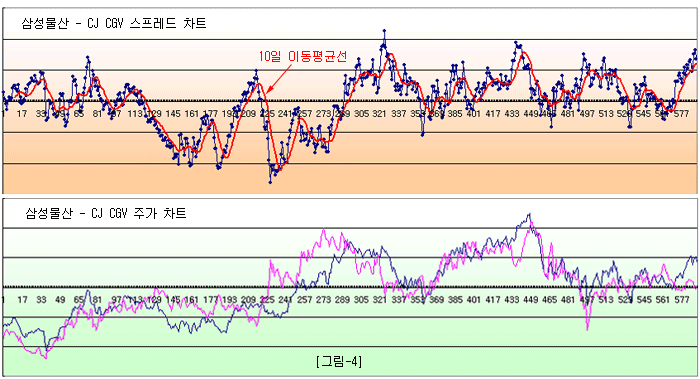
[그림-4]는 정상적인 삼성물산-CJ CGV의 페어 차트이다. 스프레드에 10일 이동평균을 취하면 [그림-3]의 스프레드와 동일할 것이다. 즉, 삼성물산과 CJ CGV 페어를 분할로 진입하면, 이동평균 스프레드에 투자하는 결과가 된다. 스프레드의 정상성은 변함이 없지만 평활 효과로 인해 변동성이 줄어든다.

이번에는 위의 논리가 일반적으로 성립하는지, 헤지 비율에 따라 결과가 달라지는지를 확인하기 위해 간단한 수식을 통해 살펴보기로 하자.

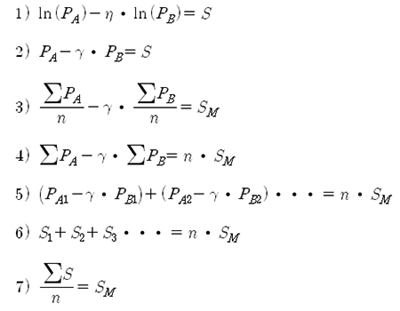
1) 식은 우리가 그 동안 봐왔던 스프레드 식이다 (S는 스프레드). 2) 식은 로그 가격차가 아닌 일반 가격의 차이다. 일반 가격차에 대한 스프레드도 Cointegration 계수가 달라지기 때문에 로그 가격에 대한 스프레드와 크게 다르지 않을 것이므로, 계산의 편의상 1)식 대신 2)식을 사용한다. 3)식은 2)식에 개별 가격 (PA와 PB) 대신에 각 페어의 이동평균 가격을 대입한 것이다. 그러면 스프레드는 S와는 다른 값인 SM이 될 것이다 (n은 이동평균 기간). 3)식을 변형하면 최종적으로 7)식을 얻을 수 있다. 7)식은 예상했던 대로 SM이 원래의 스프레드인 S의 이동평균이 된다. 또한 7)식은 헤지 비율인 Cointegration 계수와는 무관하다.

이상으로 분할 진입에 대해 알아보았다. 다시 정리해 보면 헤지 비율에 상관없이 각 종목 주가의 이동평균으로 진입하면 스프레드의 이동평균으로 진입하는 것이 된다. 이동평균에 진입한다는 것은 분할로 진입하는 것을 말한다. 완전히 이동평균을 따라 진입할 수는 없지만 (거래비용이 증가하기 때문), 여러 차례에 걸쳐 분할로 페어트레이딩을 하면 위험이 줄어든다. 또한, 진입 초기에는 헤지 비율을 맞추었지만, 시간이 지나면서 종목 가격이 변함에 따라 헤지 비율이 점점 변하는 문제도 일부는 해결된다. 분할로 추가 진입할 때 전체적인 헤지 비율을 다시 조정할 수 있는 것이다 (동적 헤지 문제).

[출처]19. 분할 페어트레이딩|작성자아마퀀트