[알고리즘 트레이딩/시장미시구조] 26. PIN 모형 (2) – 우도 함수의 설정

시장미시구조론 (Market Microstructure) – (26)

PIN 모형 (2) – 우도 함수의 설정

이전 포스트에서 설정한 PIN 모형의 파라메터 (α, δ, μ, ε)를 추정하기위해 우도 함수 (Likelihood funtion)를 설정한다. 이 파라메터들은 시장에서 직접 관찰할 수 없으므로, 관찰이 가능한 아래 데이터를 이용하여 추정하기로 한다.

아래 데이터는 2015년 3월 24일 (09:10 ~ 14:50) 삼성전자의 5분봉 데이터이다. 매 5분마다 매수, 매도량을 측정하였다. 이 날은 장중에 삼성전자 주가가 꾸준히 올랐고, 매도량에 비해 매수량이 대체적으로 높았다 (매수/매도량의 불균형). 5분 당 평균 거래량은 2,100개였고, 평균 매수량은 1,258, 평균 매도량은 842개였다. 단, 아래의 데이터는 실시간으로 체결 데이터 (XingAPI 이용)를 받아 집계한 것으로 HTS의 데이터와 차이가 날 수 있다 (수익률도 관측 시간대만 계산한 것임.).

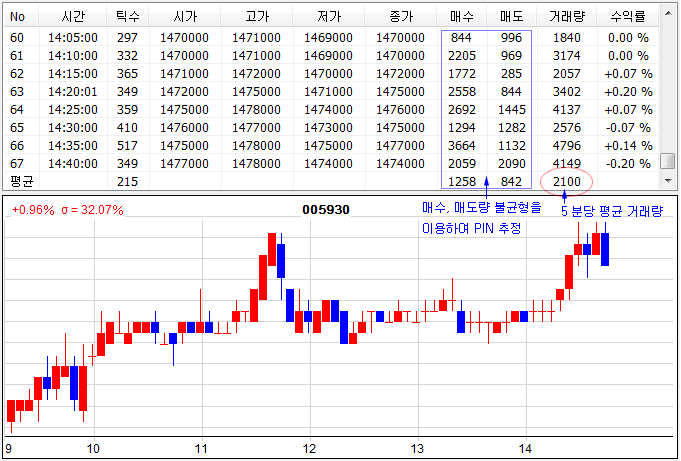
이 데이터를 이용하면 PIN 모형의 파라메터들을 추정할 수 있다. 이전 포스트에서 언급한대로 단위 시간당 발생한 거래 수량은 포아송 분포를 따른다. 여기서 단위 시간은 5분이고, 거래 수량은 매수, 매도량 혹은 거래량이 될 수 있다.

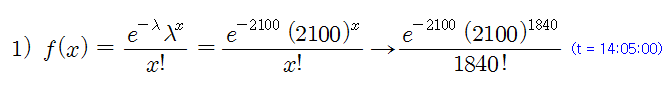
식 1)은 일반적인 포아송 분포를 나타낸 것이다. 포아송 분포의 람다 (λ)는 단위 시간당 거래 강도 (Intensity)로 5분당 발생한 평균 거래 수량을 의미한다. 이 경우 λ = 2,100이 된다. 따라서 14:05:00 ~ 14:10:00 사이에 발생한 거래량이 1,840 개가 될 확률은 식 1)로 표현할 수 있다. 단, 거래량이 발생하는 사건은 이전 시간대의 거래 사건과는 무관한 것으로 (독립 사건) 가정한다.

우도 함수의 설정 (Likelihood function)

PIN 모형의 우도 함수는 포아송 분포를 이용한다. 아래 모형에서 특정 시간대에 매수 사건이 발생하거나, 매도 사건이 발생할 확률은 f(1) ~ f(6)로 계산한다. 14:05:00 ~ 14:10:00 사이에 관측된 매수 수량 844 개는 f(1) 이나, f(3), 혹은 f(5)의 경우에 발생한 것이다. 어느 경우에 해당하는지는 모르지만, α와 δ를 추정할 수 있다면, 확률적으로 어느 경우에 발생한 가능성이 컸는지 추측해 볼 수 있다.

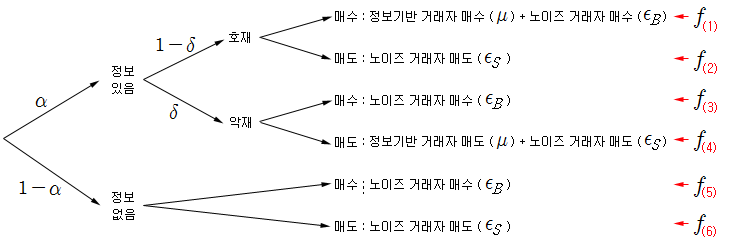
우도 함수는 아래의 식 2)로 나타낼 수 있다. 정보가 있고 (α), 호재성 정보라면 (1-δ), f(1)과 f(2)가 동시에 발생할 것이다. 만약, 정보는 있는데 (α), 악재성 정보라면 (δ) f(3)과 f(4)가 발생할 것이다. 이런 의미를 부여하면 우도 함수는 식 2)로 충분히 나타낼 수 있다.

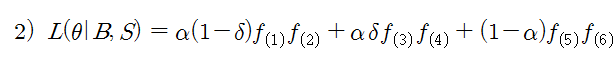
f(1) ~ f(6)는 포아송 분포를 이용하면 아래와 같이 표현할 수 있다. μ 와 ε 은 포아송 분포의 λ에 해당하는 측도이다. 즉, 단위 시간 당 발생한 매수, 매도 강도 (Intensity) 이다. 아래 식들은 위의 식 1)을 그대로 활용한 것이다.

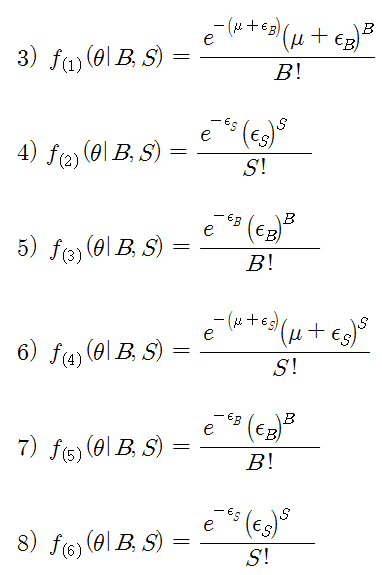
위의 식을 모두 이용하여 우도 함수를 표현하면 식 9)가 된다. μ 와 ε 은 단위 시간 당 발생한 매수, 매도 강도이고, B 와 S 는 단위 시간당 매수 수량과 매도 수량이다. μ 와 ε 은 전 시간대에 걸쳐 동일한 값이고 (단위 시간당 평균 수량), B 와 S 는 시간대에 따라 다르게 측정되는 값이다. 여기서 시장에서 관측할 수 있는 값은 B 와 S 뿐이다. 즉, B, S를 측정하여 α, δ, μ, ε를 추정하는 것이 이 함수의 목적이다.

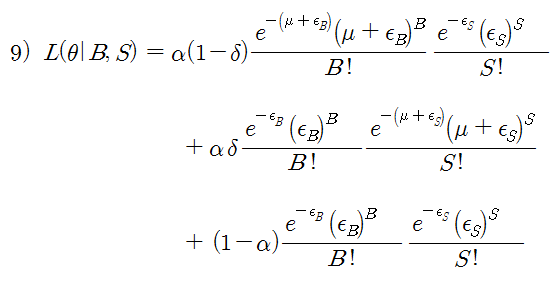
식 9)는 특정 시간대의 (예 : 09:05:00 ~ 09:10:00) 우도 함수이므로, 전체 시간대의 우도 함수를 구하려면, 특정 시간대의 우도 함수들을 모두 곱해주어야 한다. 식 10)은 각 우도 함수를 모두 곱한 것이다. 위의 경우 i= 1 ~ 67 까지 이다.

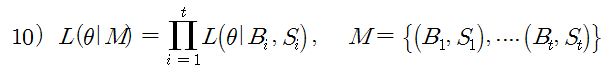
우리의 목표는 식 10) 이 최대가 되도록 α, δ, μ, ε를 결정하는 것이다. 식 10)이 최대가 된다는 것은 가장 그럴 듯해 보인다는 의미이고, 일반적으로 많이 사용하는 방식이다 (MLE : Maximum Likelihood Estimator).

그런데, 식 9)는 계산하기가 용이하지 못하다. 예를 들어 14:05:00 의 경우 1840! 을 계산하고, 2100 ^ 1840 계산하여 서로 나누어야 한다. 이 정도의 큰 수는 컴퓨터에서도 계산이 곤란하다 (Overflow 혹은 Underflow 발생). 따라서 위의 우도 함수는 계산이 가능한 식으로 변환되어야 한다. 이 부분에 대해서는 다음 포스트에서 자세히 언급하기로 한다.

참고자료:
[1] David Easley, Nicholas M. Keifer, Maureen O’Hara, Joseph B. Paperman, 1996, Liquidity, Information, and Infrequently Traded Stocks.

[출처]26. PIN 모형 (2) – 우도 함수의 설정|작성자아마퀀트