News & Events
[알고리즘 트레이딩/시장미시구조] 24. Kyle 모형 (14) – 이질적 신호를 가진 다수의 정보기반 거래자
시장미시구조론 (Market Microstructure) – (24)
Kyle 모형 (14) – 이질적 신호를 가진 다수의 정보기반 거래자
이전 시간까지는 다수의 정보기반 거래자가 서로 동일한 신호 (Homogeneous Signals)를 가진 경우에 대해 알아보았다. 이번 시간에는 다수의 정보기반 거래자가 서로 다른 신호를 (Heterogeneous Signals) 가진 경우에 대해 살펴보기로 한다.
어떤 정보기반 거래자는 정확한 신호를 가지고 있고, 어떤 정보기반 거래자는 부정확한 신호를 가지고 있다면, 두 거래자의 전략은 달라질 것이다. 전자는 공격적 전략을 취하는 반면, 후자는 덜 공격적 전략을 취하게 될 것이다. 따라서 두 거래자의 주문 수량은 달라질 수밖에 없다. 이들이 보유하고 있는 정보는 주문 수량을 통해 시장에 전달될 것이므로, 시장은 결국 이들이 보유한 신호의 정확성에 따라 영향을 받게 된다.
아래 그림은 시장에서 발생하는 사건들을 요약해 놓은 것이다. 다수의 정보기반 거래자는 각자의 신호 (u)를 가지고, 각자가 생각하는 최적의 주문 수량 (x)을 집행할 것이다. 시장에서는 총 w의 주문 수량이 관찰될 것이고, 마켓메이커는 w를 관찰하여 호가를 결정할 것이다. 다수의 정보기반 거래자 모형(2) 에서는 정보기반 거래자들이 동일한 신호를 가지고 있으므로 주문 수량이 모두 동일했지만, 여기서는 서로의 신호가 다르므로 주문 수량이 모두 다르다.
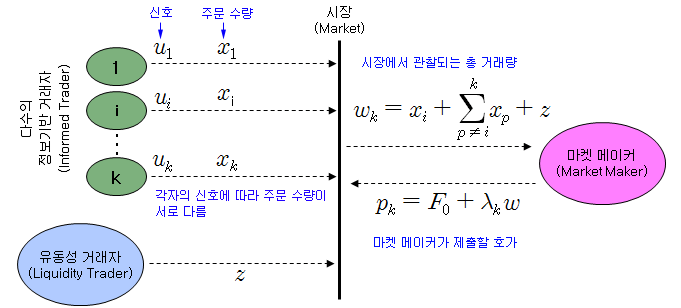
이 모형도 이전 포스트들의 논리를 확장하면 아래와 같은 결과를 얻을 수 있다 (상세 유도과정은 생략하기로 함). 시장의 충격 계수 (λ)와 정보기반 거래자의 공격성 (β)은 정보기반 거래자의 수 (k)와 신호의 정확성 (u의 분산)과 밀접한 관계가 있다.
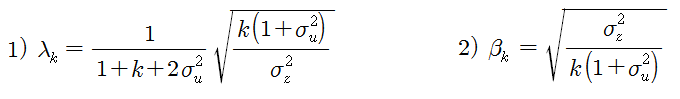
아래와 같이 그래프를 그려서 위의 결과를 해석해 보자. [그림 1]은 시장 충격 계수인 식 (1)을 그린 것이고, [그림 2]는 정보기반 거래자의 공격성인 식 (2)를 그린 것이다.
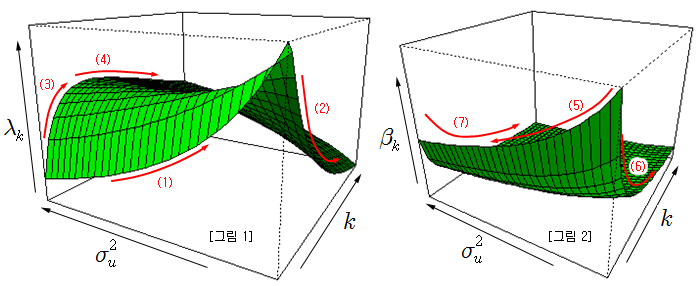
(1) 정보기반 거래자의 수 (k)가 소수일 때 신호의 정확도가 시장 충격에 미치는 영향이다. 신호 (u)의 분산이 작을수록 (신호의 정확성이 높을수록) 시장의 충격은 증가한다. 이것은 (5)번 커브와 관련이 있다. 신호의 정확성이 높을수록 정보기반 거래자의 공격성이 증가하므로, 시장의 충격은 커진다.
(2) 신호의 정확성이 매우 높은 경우에 정보기반 거래자의 수 (k)가 시장 충격에 미치는 영향이다. 신호의 정확성이 매우 높은 경우 (u의 분산 = 0)에는 k가 증가할수록 시장 충격은 감소한다. 이것은 정보기반 거래자들의 경쟁 때문에 공격성이 크게 증가하지 못하기 때문이다. 또한, 이 경우는 다수의 정보기반 거래자가 동일한 신호를 가지고 있는 경우와 동일하다. 이것은 신호의 정확성이 높을수록 신호의 이질성 효과가 사라진다는 것을 의미한다.
(3) 신호의 정확도가 매우 낮은 경우 (u의 분산이 큰 경우)에 정보기반 거래자의 수 (k)가 시장 충격에 미치는 영향이다. k가 낮은 곳에서는 k가 증가할수록 시장 충격은 증가한다. 이것은 k가 낮은 곳에서는 경쟁 효과보다 (신호의 정확도가 낮으므로), k가 시장 충격에 미치는 영향이 더 크기 때문이다.
(4) (3)의 경우에서 k가 높은 곳에서는 k가 증가할수록 시장 충격은 서서히 감소한다. 이것은 k가 증가할수록 경쟁효과가 점점 커지기 때문이다.
(5) 정보기반 거래자가 소수일 때는 신호의 정확성이 높을수록 정보기반 거래자의 공격성이 증가한다.
(6) 신호의 정확도가 매우 높은 경우에는 (u의 분산 = 0) k가 증가할수록 정보기반 거래자의 공격성은 감소한다 (경쟁 때문임).
(7) 신호의 정확도가 매우 낮은 경우에도 k가 증가할수록 정보기반 거래자의 공격성은 감소한다. 그러나 (6)의 경우보다는 공격성의 수준도 낮고 공격성이 감소하는 정도도 완만해 진다. 이것은 신호의 정확도가 낮으면 공격성이 작아지고, k가 증가할수록 공격성이 작아지므로, 두 효과가 겹쳐서 나타나기 때문이다.
여기까지 14편의 포스트를 통해 Kyle의 기본모형 + 확장모형에 대해 살펴보았다. Kyle의 모형은 시장의 참여자가 서로 전략적으로 최선의 이득을 취하려는 경쟁 모형 (불완전 경쟁)이고, 이 과정에서 시장이 균형을 이루어가는 과정을 모형화한 것이다. 완전한 시장을 그릴 수는 없겠지만, 모델을 통해 개략적인 시장의 모습을 그려볼 수 있다는 것이 매우 흥미롭다.
Kyle의 확장 모형에서는 주로 정보기반 거래자를 중시하여 시장을 묘사해 왔다. 이것은 정보기반 거래자가 시장에 미치는 영향이 크기 때문일 것이다. 그러면 현재 시장에 참여하고 있는 정보기반 거래자가 얼마나 되는지 추정해 볼 수 있을까? 실제 시장 데이터를 이용해서 k의 규모를 추정할 수 있다면 현재 시장의 특성을 좀 더 자세히 알 수 있을 것이다.
k를 추정하는 방법으로 대표적인 모형으로는 Easley 등이 제안한 PIN (Probability of Informed Trader)/VPIN 모형이 있다. 다음 시간부터는 PIN/VPIN 모형에 대해 자세히 살펴보기로 한다.
