News & Events
[알고리즘 트레이딩/시장미시구조] 12. Kyle 모형 (2) – 기본 모형의 파라메터 결정 (6)
시장미시구조론 (Market Microstructure) – (12)
Kyle 모형 (2) – 기본 모형의 파라메터 결정
이번 시간에는 지난 시간에 설정한 Kyle의 기본 모형에서 설정한 β와 λ를 결정하여 Kyle의 기본 모형을 완성해 보기로 한다. 지난 시간에 언급한대로 β는 정보기반 거래자의 공격 성향을 의미하고, λ는 마켓메이커의 Pricing에 의한 시장 충격을 의미한다.
1. 정보기반 거래자의 최적 주문량 결정
정보기반 거래자는 자신이 알고 있는 정보가 시장에 노출되는 것은 최소화하면서, 수익은 극대화 시키는 것을 목표로 한다. 정보기반 거래자는 시장에서 거래되는 자산의 가격이 자신이 알고 있는 자산의 가치보다 낮다고 해서 무턱대고 매수 주문을 낼 수는 없다. 마켓메이커가 제시하는 가격 (p)을 살펴가면서 적당량의 주문을 (x) 내야 하는 것이다.
아래의 식 1)은 정보기반 거래자가 x 만큼 매수했을 때의 수익 (Profit)을 나타낸다. F는 자신이 알고 있는 자산의 미래 가치이고, p는 현재 마켓메이커가 유동성을 공급한 가격이므로, 현재 x 만큼의 주식을 가격 p에 매수하고, 향후 가격이 F가 되었을 때 매도하는 것을 가정하여 계산한 것이다 (주-1).
식 2)는 마켓메이커가 유동성을 공급하는 가격을 나타낸다. 마켓메이커는 시장에 유입된 주문 (x + z)을 관찰하여 유동성을 공급할 최적 가격을 결정한다.
식 3)은 정보기반 거래자의 기대 수익을 나타낸다. 자신이 알고 있는 미래의 자산 가치 (F)에 대한 수익의 조건부 기댓값으로 나타낸다. 이 기댓값이 최대가 되도록 x를 결정하면, 이 x 가 최적 주문량이 된다. 식 3)은 p에 대한 함수이므로, p가 변함에 따라 최적 주문량인 x도 변하게 된다. 또한, 식 3)에 식 2)를 대입하면 식 3)은 x와 z에 대한 함수가 되므로, 자신이 주문한 수량 (x)이, 다음 번 주문 수량에 영향을 미치게 된다 (Recursive).
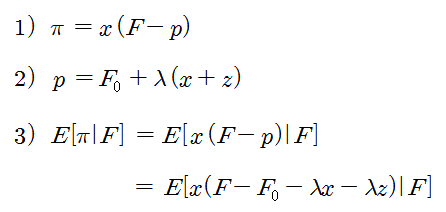
주문 수량 x의 변화 대해 식 3)이 최대가 되려면, 아래 식 4)의 관계가 성립한다 (E[F|F] = F, E[z] = 0 이 이용되었음). 식 4)로부터 x를 결정하면 식 5)가 되고, 우리가 결정하려고 했던 두 파라메터의 관계는 식 6)과 같이 된다. 식 6)은 시장 충격이 클수록 정보기반 거래자의 공격성이 작아짐을 의미한다. 즉, 마켓메이커에 의해 제시되는 가격의 편차가 커지면 정보기반 거래자의 공격성이 줄어들고 주문 수량은 줄어들게 된다.
2. 마켓메이커의 최적 호가 결정
마켓메이커 입장에서는 시장에 유입되는 주문량을 (w = x + z) 관찰하여, 최적 호가를 결정해야한다. 마켓메이커는 미래 주가 (F)에 대한 정보가 없으므로, 시장의 주문량을 관찰하여 F를 추정해야 한다. 따라서 공급 가격 p는 w (혹은 x + z)의 함수가 된다. 유동성 공급 가격은 w를 관찰하여 정보기반 거래자가 알고 있는 F를 알아내는 과정이므로, 식 7)과 같이 w에 대한 F의 기댓값으로 나타낼 수 있다. 식 7)을 풀기 위해 식 8) ~ 10)의 과정을 이용한다. 식 9)에서 x 와 z는 서로 독립이므로 공분산은 0 이 되고, 식 10)에서도 F와 z의 공분산은 0 이 된다.
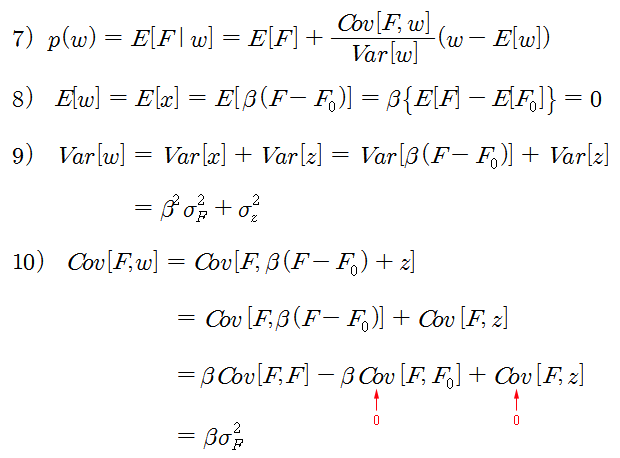
식 8) ~ 10)의 과정을 이용하면 식 7)은 식 11)로 표현할 수 있다. 식 11)을 이용하면 λ와 β의 관계를 구할 수 있고, 식 6)을 이용하면 λ와 β를 구할 수 있다 (식-13).
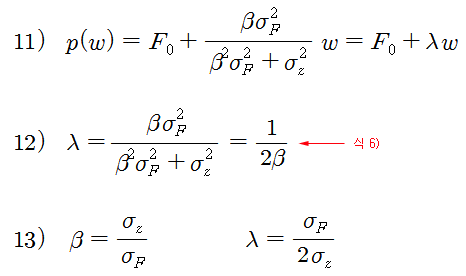
결정된 λ와 β를 이용하면, 최종적으로 정보기반 거래자의 최적 주문량과, 마켓메이커의 최적 호가를 결정할 수 있다. 아래의 식 14)는 마켓메이커가 결정한 최적 호가이고, x와 z의 함수로 표현된다. 시장에 유입된 총 주문 (x + z)을 이용하여 호가를 결정한 것이다. F0는 최근 거래 가격의 평균치이고, 시장에 매수 주문 (x + z > 0)이 유입된 경우라면, 결정된 호가는 최근의 주가보다 높을 것이다. 반대로, 시장에 매도 주문이 유입된 경우라면 (x + z < 0) 호가는 최근 주가보다 낮을 것이다. 식 15)는 정보기반 거래자의 최적 주문량이고, F의 함수가 된다.
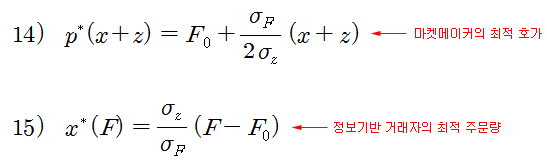
이번 시간에는 단순히 수학적 논리로 정보기반 거래자의 최적 주문 수량과, 마켓메이커의 최적 공급 가격을 구해 보았다. 다음 시간에는 이 결과가 의미하는 것이 무엇인지 직관적으로 해석해 보기로 한다.
(주-1) 위의 식에서 F, z, w, x, p는 확률 변수이고, 나머지 변수는 상수를 의미한다. 보통의 경우 확률 변수는 ‘~’ 표시를 붙여 구분하기도 하는데, 이것은 계산 시 혼돈되지 않도록 하기 위함이다. 그러나 여기서는 표기의 간결성을 위해 이를 구분하여 표기하지 않았다. 이 구분이 필요한 이유는 다음과 같다. 만약 w 가 확률 변수라면 E[w] = w의 평균 (i.e. w0) 이나, w가 상수라면 E[w] = w 가 된다. 따라서 변수가 확률 변수인지 상수인지 구분하여 표기하는 것이 필요하다.
