News & Events
[알고리즘 트레이딩/시장미시구조] 8. Madhavan 모형 (1) – 주가 모형 설정
- 2019년 1월 11일
- Posted by: 인사이트캠퍼스
- Category: 금융/AI/IT 기사

시장미시구조론 (Market Microstructure) – (8)
Madhavan 모형 (1) – 주가 모형 설정
거래 데이터를 직접 관찰하여 시장을 직관적으로 이해하는 것도 중요하지만, 시장의 내면을 좀 더 깊이 이해하기 위해서는 이론적인 모형을 통해 시장을 해석해 볼 필요도 있다. 시장미시구조론에는 시장의 미세 구조와 주가의 생성 원리를 밝히기 위해 많은 모델이 개발되어 있다. 이번 시간에는 첫 번째 모형으로, 지난 시간에 살펴본 시장가 주문의 연속성과 관련된 모형에 대해 살펴보기로 한다.
Madhavan은 1996년 “Why Do Security Prices Change?” 라는 논문에서 주가가 형성되는 원리를 설명하고 스프레드와 변동성을 여러 요인별로 분해하는 작업을 하였다. Madhavan은 공공 정보 (News)의 발생과 시장 참여자의 거래 행위로 인해 주가가 변화하고, 변동성이 발생하는 것으로 보고 시장의 특성을 설명하였다. 즉, 주가 변화와 변동성 발생 요인을 News와 거래 행위로 구분하고, 각 요인이 주가와 변동성에 미치는 영향을 분석하였다.
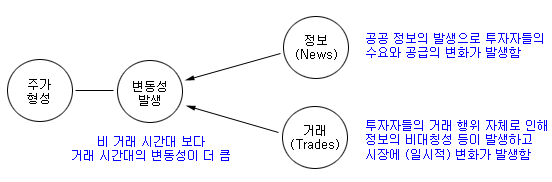
변동성의 원인은 호재나 악재 같은 공공 정보의 발생 요인과 거래 행위 자체로 인한 요인으로 구분해볼 수 있다. 그럼 둘 중에 어느 요인이 변동성에 더 큰 영향을 미치게 될까? 결과는 거래 행위 요인이 변동성에 더 큰 영향을 미치는 것으로 알려져 있다. 이에 대한 실험으로 (1) 주가의 월요일 종가와 화요일 종가로 계산한 수익률 분산과 (2) 금요일 종가와 월요일 종가로 계산한 수익률 분산을 비교해 본 결과가 있다. 거래 일수는 모두 1일 이지만, 달력 일수로는 (1)은 1일이고, (2)는 3일이다. 만약 수익률 분산이 News에 의해서만 발생한다면 (2)의 분산이 (1)의 분산보다 3배 정도 커야 한다. 그러나 실험 결과는 불과 20% 정도 큰 것으로 나타났다. 그렇다면 변동성은 거래 행위 자체에 더 큰 영향을 받는다고 볼 수 있다. (출처 : 달러옵션 전략 p.97, 우대성, 2010)
Madhavan은 주가 모형을 아래 그림과 같이 표현 하였다. t-시점에 기대되는 적정 주가는 이전의 기대 주가에서 거래 행위로 인한 부분과 공공 정보로 인한 부분만큼 변화하는 것으로 모형화 하였다. 주가에 긍정적인 정보가 발생한다면 현재 주가는 이전 주가보다 상승할 것이고, 참여자들의 거래 행위가 주가에 긍정적으로 작용한다면 현재 주가는 상승할 것이다.
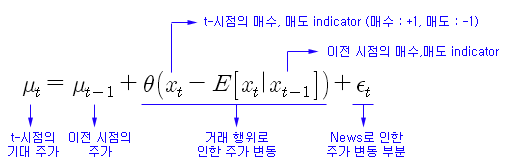
공공 정보 (News) 부분은 표준 정규분포를 따르는 잔차 성분으로 본다. 즉, 호재가 발생할 확률과 악재가 발생할 확률은 서로 동일하고, 극단적 호재나 악재가 발생할 확률은 정규분포에 따라 점차 낮아지는 것으로 가정한다. 거래 행위로 인한 부분은 위의 수식과 같이 시장가 주문의 상황으로 표현한다. 시장가 매수 주문이 연속적으로 유입되면 주가는 상승하려는 경향이 있을 것이고, 매도 주문이 연속적으로 유입되면 주가는 하락하려는 경향이 있을 것이다. 만약, 거래 행위로 인한 부분이 0 이라면 주가의 차분 값은 잔차 성분만 가지므로 주가는 랜덤워크를 따르게 된다.
거래 행위로 인한 부분에서 기댓값 부분은, 이전 시점의 시장가 주문을 관찰한 상태에서, t-시점에 발생할 시장가 주문의 기대치이다. 만약, t-시점에 시장가 매수 주문이 발생할 것으로 기대했는데, 실제로 시장가 매수 주문이 발생했다면 (E[ ] = +1, xt = +1) 거래 행위로 인한 부분은 0 이 된다. 그러나 시장가 매수 주문이 발생할 것으로 기대했는데, 실제로는 매도 주문이 발생했다면 (E[ ] = +1, xt = -1) 거래 행위로 인한 부분은 2*θ가 된다. 즉, 기대와는 다른 상황이 발생한 것이고 (Surprise 발생) 주가는 영향을 받게 된다. 여기서 () 안의 부분은 Surprise 혹은 정보의 비대칭성 (Information Asymmetry)을 나타내고, θ는 정보의 비대칭이 주가에 미치는 영향의 정도를 나타낸다.
이번에는 마켓메이커가 시장에 존재한다고 보고, 마켓메이커가 유동성을 공급할 호가를 표현해 본다. 마켓메이커는 유동성을 공급하는 대가로 적정 주가보다 높은 가격에 지정가 매도 주문을 낼 것이고, 적정 주가보다 낮은 가격에 지정가 매수 주문을 낼 것이다. 물론, 이 대가는 비 마켓메이커인 일반 투자자에게는 거래 비용으로 작용할 것이다.
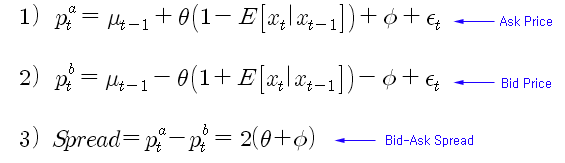
마켓메이커는 위의 식과 같이 Ask 및 Bid Price를 제출하는 것으로 가정해 본다. Ask Price의 경우 이전 시점의 적정 주가보다 기본적으로 φ 만큼의 대가를 요구한다. 또한, 정보의 비대칭 정도에 따라 추가의 프리미엄을 요구하게 된다. 만약, t-시점에 시장가 매수 주문이 발생할 것으로 기대했다면 (E[ ] = +1), 실제로는 매수 주문이 발생했으므로 정보의 비대칭에 대한 추가 프리미엄은 0 이 된다. 그러나 t-시점에 시장가 매도 주문이 발생할 것으로 기대했다면 (E[ ] = -1), 실제로는 매수 주문이 발생했으므로 2*θ 만큼의 추가 프리미엄을 요구한다. (Bid-price 도 같은 논리로 설명됨)
위의 수식을 그림으로 표현해 보면 아래 그림과 같이 된다. 마켓메이커는 적정 주가에 기본적인 대가 (φ)와, 정보의 비대칭에 대한 추가 프리미엄을 요구하여 적정 호가를 계산한다. 기본적인 대가 (φ)는 유동성 공급에 대한 대가로, 마켓메이커의 영업비용, 재고 부담에 따른 대가 등으로 구성된다. 그리고 일반 거래자가 부담해야할 비용인 Bid-Ask 스프레드는 식 3)과 같이 계산된다.
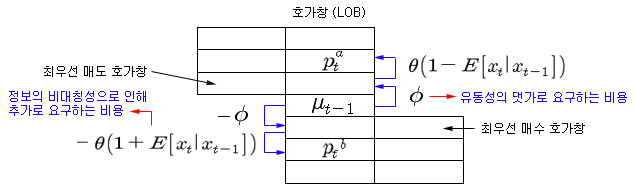
거래 가격을 기준으로 주가를 표현하면 아래의 식 4)와 같이 된다 (Transaction price). 이 식은, 현재 거래가 이루어지는 가격 (pt)은 적정 가격에 주 당 φ 만큼의 비용이 추가되는 것을 의미한다. 만약 누군가가 시장가 주문으로 1 주를 매수할 경우 (xt = +1)에는 현재의 적정 가격보다 φ 만큼 높은 가격에 매수해야할 것이고, 1 주를 매도할 경우 (xt = -1)에는 적정 가격보다 φ 만큼 낮은 가격에 매도해야할 것이다.

식 4)와 맨 위의 식을 조합하면 식 5)를 얻을 수 있다. 여기서 시장가 주문의 indicator인 xt가 AR(1) 과정을 따른다면, 식 5)의 기댓값 부분은 식 6)과 같이 표현할 수 있다. 이 표현은 AR(1) 모형의 제 1단계 전방 예측값이다. 이전 포스트의 시장가 주문의 연속성에서 살펴보았듯이 시장가 주문 indicator는 AR(1) 모형을 따르는 것으로 보아도 큰 무리가 없다. 식 5)에 식 6)과 4)를 적용하면 최종적으로 식 7)을 얻을 수 있다. 이 식이 바로 Madhavan이 설정한 주가 모형이다.
현재 거래 가격은 이전 거래 가격에서 마켓메이커의 비용 (φ), 정보의 비대칭 정도 (Θ), 시장가 주문의 연속성 (ρ), 그리고 공공 정보의 발생 효과 (ε) 만큼 변화가 발생한다. 이 식과 실제 시장 데이터를 이용하면 각 요인을 추정해 볼 수 있고, 각 요인별로 주가에 미치는 영향의 정도를 추정해 볼 수 있다. 다음 시간에는 식 7)의 모형에 포함된 각 파라메터를 추정해 보고, 실증 분석을 통한 추정 결과를 확인해 보기로 하겠다.
Reference : Why Do Security Prices Change? A Transaction-Level Analysis of NYSE stocks.
(Madhavan, Anath, Matthew Richardson and Mark Roomans, 1996 )

