[알고리즘트레이딩/전략편] 08. 알고리즘 트레이딩 – 옵션의 페어트레이딩 (2)

알고리즘 트레이딩 (Algorithmic Trading) – 전략 (8)

알고리즘 트레이딩 – 옵션의 페어트레이딩 (2)

“이 전략은 본 블로그의 페어 트레이딩 기초편 (1~9)의 사전지식을 요합니다.”

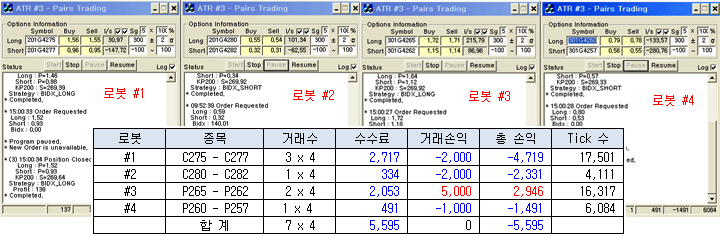
이전 포스트에서 작성한 자동매매 시나리오로 4대의 로봇을 1일간 가동시켜 (2012년 3월 28일, 5시간 40분) 아래와 같은 결과를 얻었다. 스프레드 계산 시 현재가를 이용하지 않고, 호가창에 있는 즉시 매수/매도 가능한 가격을 이용하였기 때문에, 스프레드의 상한선과 하한선을 초과하는 경우가 드물게 검출되었다. 이는 호가 스프레드의 손실을 줄이기 위한 방편이다.

거래 종목은 콜옵션 4개와 풋옵션 4개를 이용하여, 아래와 같이 페어로 구성하였다. 거래는 각 옵션 당 1계약씩 하였고, 7번의 매수/매도 페어가 발생하였으므로, 총 28번 옵션이 매매 되었다. 그림에서와 같이 거래 손익은 0원 이었으며 수수료만큼 손실을 보았다. 거래 횟수가 워낙 적어 이 결과만으론 결론을 낼 수는 없으나, 필자가 그동안 시험해 본 결과도 거의 이와 같은 패턴의 손익구조를 보였었다.

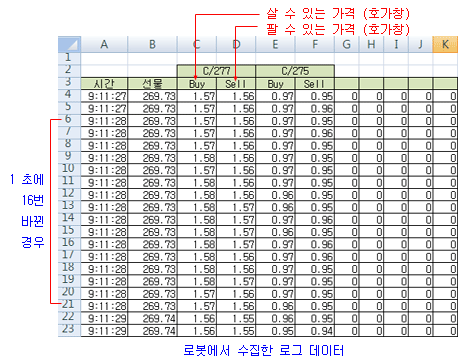
자세한 결과 분석을 위해 각 로봇에서 수집한 로그 데이터를 분석해 보자. 로그 데이터는 아래 그림과 같이 동일 시간대에 수집된 페어 종목의 가격들이다. 종목 별로 즉시 사고 팔 수 있는 가격을 기준으로 하였기 때문에, 이중 1개의 가격만 바뀌어도 스프레드는 1틱이 바뀌므로, 스프레드의 계산은 매우 빈번히 이루어진다. 아래 그림에서는 1초에 16번 바뀐 경우도 있었다. 로봇의 순간 포착 능력을 위해 모든 데이터는 틱-데이터로 분석하였다. 물론, 이동평균, 표준편차, 이론가 계산을 위해서는 모두 실시간 스트림 계산 알고리즘을 사용해야 한다. 로봇 #1의 경우는 5시간 40분 동안 총 17,501개의 틱-데이터를 수집하였다.

아래 그림은 수집된 로그 데이터를 분석한 결과이다. 그림 (가)는 옵션의 가격을 이용하여 계산한 페어트레이딩의 스프레드 차트이고, 그림 (다)는 각 옵션의 주가 차트이다. 그림 (나)는 뒷부분에 상세히 설명하겠지만 옵션의 이론가를 고려한 스프레드 차트이다. 그림 (라)는 이론가로 계산된 진입 시 예상되는 손익구조이고, 그림 (마)는 실제로 측정된 손익구조 이다.

우선, 주목해야 할 것은 그림 (가)와 (다)의 패턴이 동일하다는 것이다. 원래 페어 트레이딩의 스프레드는 주가의 변동에 영향이 없어야 한다. 그러나 옵션의 스프레드는 주가의 영향을 그대로 받아, 주가가 오르면 스프레드도 오르고, 주가가 내리면 스프레드도 같이 내린다. 이것은 포지션 진입 후의 손익이 주가의 흐름에 그대로 노출된다는 것이다. 따라서 페어 트레이딩의 효과는 사라지고, 주가의 방향에 따른 Naked 매매가 되어 버린다. 오히려 상호 헤지로 인해 Naked 매매 보다 더 불리한 상황이 되어 버린다.

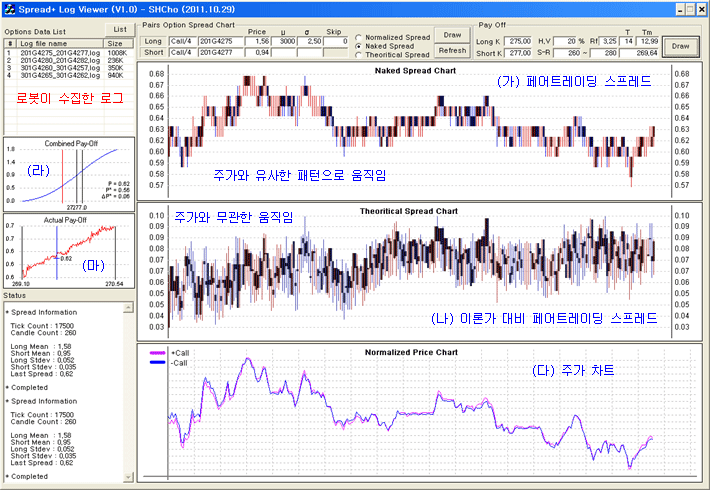
그림 (라)는 포지션 진입 후의 예상되는 손익구조이다. 앞에서 언급한데로 주가가 오르면 포지션의 손익도 증가하고, 주가가 내리면 손익은 감소한다. 그림 (마)는 실제 측정한 손익구조이다. 그림 (라)에서 예상한 바와 유사하게 측정된다. 따라서 이 전략은 이전 포스트에서 예상한데로, 옵션의 델타 값의 차이로 인해 주가에 무관한 (정상성을 갖는 혹은 평균 회귀 성질을 갖는) 스프레드를 만들 수 없다.

흥미로운 것은 옵션의 이론가를 고려하여 만든 그림 (나)의 스프레드이다. 스프레드가 주가와는 무관하게 움직이고 있다. 따라서 이 스프레드를 이용하면 주가에 무관한 시장중립효과를 볼 수 있을 것으로 기대된다.

 그림 (나)는 아래의 원리로 만들어진 스프레드이다. 스프레드가 주가의 영향을 받는 것은 옵션의 볼록성 때문이다 (델타 값이 일정치 않음). 만약 볼록성 효과를 제거할 수만 있다면 주가의 영향을 받지 않는 스프레드를 만들 수 있을 것이다. 아래 식에서 (1)은 위의 그림 (가)의 스프레드이며, 볼록성에 의한 자연스러운 괴리와 수급에 의한 일시적 괴리의 합으로 구성된다고 볼 수 있다. 볼록성에 의한 당연한 괴리는 식 (2)와 같이 두 옵션의 이론가의 괴리로 표현할 수 있다. 따라서 식 (1)에서 볼록성에 의한 괴리를 제거한 스프레드를 만들면 식 (3)과 같이 된다.

그림 (나)는 식 (3)으로 표현한 스프레드이며, 예상과 같이 주가의 영향을 받지 않고, 일시적인 수급에 의한 괴리만 보이고 있다. 이 스프레드에 페어 트레이딩에서와 같이 균형점, 진입선, 청산선을 설정할 수 있다.

이 전략은 이론가 계산, 균형점, 진입선, 청산선 설정의 변화로 결과가 달라질 수 있다. 필자의 경우는 로봇에서 잔존기간, 이자율, 변동성 등의 연속적 변화를 고려하여 이론가를 계산하고 있다. 또한, 실시간 데이터 스트림 분석에 의한 균형점 설정 같은 미세한 변화로 인해 결과를 속단하기는 어려운 상태이다.

이 전략은 필자도 아직 결론을 내지 못한 상황으로, 지금 자세히 언급하기는 어렵다. 따라서 관심 있는 독자 분들의 도전을 기대하면서 미결 상태로 남겨 두고자 한다.

2012.07.02 Update:

이 전략에서는 호가 스프레드 손실을 줄이기 위해 시장가 주문을 기준으로 스프레드를 계산하였기 때문에 주가 흐름에 무관한 정상성을 갖는 스프레드를 만들지 못했다. 이것을 지정가 주문 방식으로 바꾸면 정상성을 갖는 스프레드를 만들 수 있다. 롱-숏의 지정가 주문 체결은 마켓메이킹 전략의 주문 체결율에 따라 결정되기 때문에 마켓메이킹 전략과 결합한 형태도 고려해 볼 수 있다. (옵션의 페어트레이딩과 마켓메이킹의 결합 전략 참조)

[출처]8. 알고리즘 트레이딩 – 옵션의 페어트레이딩 (2)|작성자아마퀀트