News & Events
[금융수학] 40. 델타 헤지 옵션의 손익 (1) – 실현변동성을 이용한 델타 헤지
금융수학 (40)
델타 헤지 옵션의 손익 (1) – 실현변동성을 이용한 델타 헤지
이번 시간에는 옵션의 델타 헤지를 이용한 변동성 거래에 대해 알아보기로 한다. 이전 시간에 언급한대로 옵션의 기초자산 (S)을 연속적으로 델타 헤지 (Hedge)하면 옵션을 복제할 수 있다. 그런데 델타를 계산할 때 옵션에 내재된 변동성 (Implied volatility)을 사용할 것인지, 역사적 변동성 (Historical volatility)을 사용할 것인지, 아니면 (알 수는 없지만) 미래의 실현변동성 (Realized volatility, 혹은 actual volatility)을 사용할 것인지에 대해 생각해 볼 필요가 있다. 이번 시간에는 실현변동성을 사용한 경우의 특성에 대해 살펴보기로 한다 (물론, 미래의 실현변동성을 알고 있다고 가정한다).
현재 옵션에 내재된 변동성이 향후 발생할 실현변동성에 비해 현저히 높다고 가정해 본다 (실현변동성을 알고 있다고 가정). 그렇다면 현재의 옵션 (Vi)은 실현변동성으로 평가된 옵션 (Vr)보다 고평가 되어 있다고 볼 수 있다. 따라서 이 상황은 식 1)로 표현할 수 있다 (여기서 아래 첨자인 i 는 Implied volatility를 의미하고, r 은 Realized volatility를 의미한다).
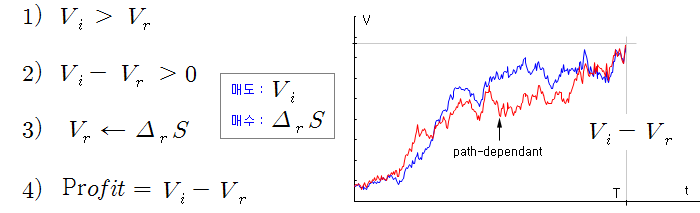
고평가된 옵션 (Vi)을 매도하고 정상적으로 평가된 옵션 (Vr)을 매수한다면 (Vi – Vr) 만큼의 차익을 기대할 수 있다. 그리고 기초자산 (S)를 이용하여 실현변동성을 기준으로 연속 델타 헤지를 하면 (ΔS) 정상적으로 평가된 옵션 (Vr)을 복제할 수 있다. 따라서 만기까지 (Vi – ΔS) 포지션이 유지되도록 연속 델타 헤지를 한다면 (Vi – Vr) 만큼의 수익을 기대할 수 있다. 왜냐하면 현재 고평가된 (Vi)는 만기시 실현변동성으로 평가된 가치 (Vr)로 수렴할 것이기 때문이다.
현금 흐름을 통해 델타 헤지 거래를 정리하면 아래 표와 같다. t0 시점에 고평가된 옵션을 매도하고 (- Vi), 델타만큼 주식을 매수한다 (+ΔS). 이 때 델타는 실현변동성 (Realized volatility)을 기준으로 적용한다. dt 시간 후에는 각 자산의 가치가 변화하므로 현금 흐름의 총합에 변화 (dπ) 가 생긴다 (여기서 r 은 무위험 수익률을 의미함).
이제 dπ 를 계산해 보자. dπ 는 dt 시간 동안의 P&L이 되고 (dt 가 1 day 이면, dπ 는 daily profit 이 된다). dπ 는 식 5)로 쓸 수 있고, 각 자산의 변화는 식 6)과 식 7)로 쓸 수 있다. 여기에 GBM (기하브라운운동) 모형과 블랙-숄즈의 편미분 방정식을 이용하면 최종적으로 식 14)를 얻을 수 있다.
식 14)는 변동성 차익거래로 나타난 profit 이다. 그런데, 이 식에는 dW (W : Weiner process) 항이 포함되어 있으므로 dπ 는 dW 의 영향을 받아 Random path를 구성한다 (path-dependant). 그러나 만기시 총 profit은 정확히 (Vi – Vr)이 된다. 만기 이전에 청산하는 경우라면 profit은 정확히 (Vi – Vr)이 되지 않고 dW 에 따라 결과가 다르게 나타난다.
아래 그림은 at-the-money 옵션을 이용하여 1,000 번의 델타 헤지를 적용한 시뮬레이션 결과이다 (출처 : 아래 참고자료). 이 결과는 옵션의 내재변동성이 실현변동성에 비해 현저히 낮아 저평가된 옵션을 매수하고 (+Vi), S를 델타만큼 매도한 (-ΔS)경우의 시뮬레이션 결과이다 (위의 수식과는 반대의 경우임).
* 실현변동성 = 30%
* 내재변동성 = 20% ~ 실현변동성보다 10% 낮음 : 옵션이 저평가 되었음.
* S의 drift = 10%
* 무위험 수익율 = 5% ~ 주식의 drift 와 무위험 수익률 (r)이 다른 경우임.
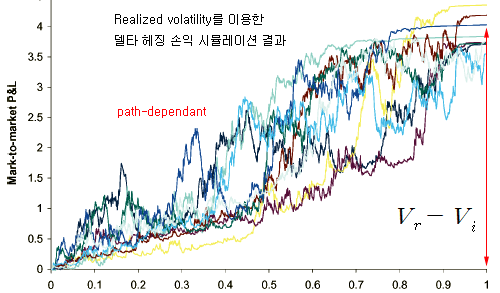
P&L for a delta-hedged option on a mark-to-market basis, hedged using actual volatility.
[그림 출처 : 아래 참고자료의 Figure 2]
시뮬레이션 결과 만기까지의 최종 수익률은 거의 (Vr – Vi) 이다. 정확히 (Vr – Vi)이 되지 않는 이유는 연속 델타 헤징이 아니라 이산 델타 헤징 (1,000 번)을 적용했기 때문이다 (헤지 오류 발생). 그리고 만기시에는 (Vr – Vi)의 수익을 보장하지만 중간의 모든 경로가 일치하지는 않는다. 이것은 dW 항 때문에 발생하는 현상이다 (path-dependant).
참고자료 : Paul Wilmott, Wilmott magazine : Which Free Lunch Would You Like Today Sir? : Delta Hedging, Volatility Arbitrage and Optimal Portfolios
