[금융수학] 36. 내재변동성 곡선 추정식 (SVI)

금융 수학 (36)

내재변동성 곡선 추정식 (SVI)

지난 시간에 이어 내재변동성 스마일 곡선의 추정식에 대해 알아보기로 한다. 내재변동성 곡선의 추정식으로는 1999년 메릴린치의 Jim Gatheral에 의해 고안된 Stochastic Volatility Inspired (SVI) 가 유명하다. Jim Gatheral은 현재 Baruch College의 교수로 변동성의 권위자로 알려져 있고, 현재도 SVI surface 모형을 꾸준히 연구하고 있다.

아래 식은 1999년에 고안된 단일 월물의 옵션 가격으로 내재변동성 곡선을 추정한 식이다. 여러 월물의 옵션을 이용하면 (근월물, 차월물 …) 곡선이 아닌 Surface 형태로도 추정이 가능하다. 이 식은 5개의 파라메터 (a, b, ρ, m, σ)로 변동성을 표현하고 있다 (우변의 σ 는 변동성이 아닌 파라메터임). k 는 Moneyness로 행사가격 (X)과 선물 가격으로 계산한 것이다. 이 식은 분산 (변동성의 제곱)을 k의 함수로 표현한 것이다.

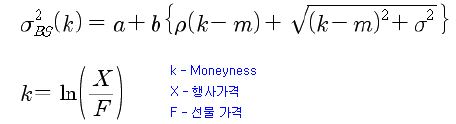
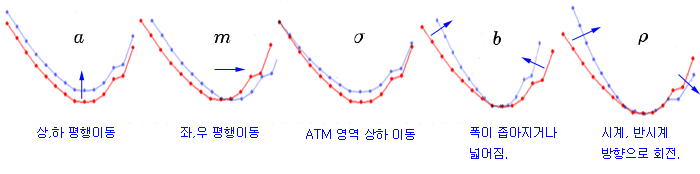
5개의 파라메터 (a, b, ρ, m, σ)는 아래 그림과 같이 고유한 특성을 가지고 있다. a가 변화하면 내재변동성이 상,하로 평행이동하고, b가 변하면 좌, 우로 평행이동한다 (나머지는 그림 참조). 만약 시장에서 관측된 내재변동성으로 위 식의 5개의 파라메터를 추정할 수 있다면, 시장에서 내재변동성이 변화하는 모습을 관찰할 수 있다. 예를 들어 시간이 지남에 따라 ρ 가 점차 작아진다면 내재변동성 곡선은 시계 방향으로 회전하고 있다는 것을 알 수 있다. 즉, Put OTM 영역의 내재변동성은 커지고, Call OTM 영역의 내재변동성은 작아지고 있다는 것을 알 수 있다.

5개의 파라메터 (a, b, ρ, m, σ)를 추정하려면 실제 관측된 내재변동성과 SVI 이론식의 오차가 최소가 되도록 수치해석을 이용해야 한다. 2004년 Jim Gatheral이 소개한 논문에서는 GMM (Generalized Method of Moments) 방법을 이용하였으나, 여기서는 간단히 OLS (Ordinary Least Square) 방식으로 파라메터를 추정해 보기로 한다.

추정해야할 모수가 5개로 6차원 공간에서 최소점을 찾아야 하므로, 추정의 정확도가 문제가 될 수 있다. 초기값 설정에 따라 지역적 최소값 (Locally minimum)이 나올 수도 있다. 전체 영역에서의 최소값 (Globally minimum)을 찾기 위해서는 수치해석을 어떻게 설계할 것인가도 관건이다. Jim Gatheral은 차익거래가 발생하지 않는 조건으로 (No arbitrage condition) 각 파라메터의 영역을 제한하였고, 초기값은 아래와 같이 설정하였다.

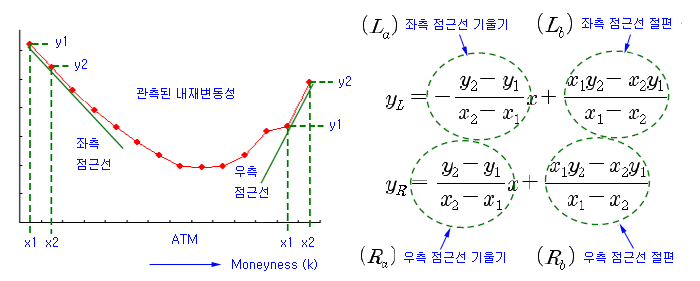
내재변동성 곡선은 일반적으로 U-자형과 유사한 형태이므로, 좌측 점근선과 우측 점근선을 갖는 쌍곡선 형태로 초기값을 설정한다. 위 그림과 같이 내재변동성의 좌측 2점 (Put 옵션의 좌측 2점)을 지나는 직선의 방정식을 좌측 점근선으로 설정하고, 우측 2점 (Call 옵션의 우측 2점)을 지나는 직선의 방정식을 우측 점근선으로 설정한다. 그리고 각 파라메터의 초기값은 아래와 같이 각 점근선의 기울기와 절편을 이용하여 계산한다. 관측된 내재변동성이 불규칙해서 점근선이 이상하게 나올 수도 있다 (예 : 좌측 점근선의 기울기가 + 이거나, 우측 점근선의 기울기가 – 임). 이런 경우를 대비해서 2점이 아닌 3~4개의 점으로 회귀식으로 점근선을 구하기도 한다.

위와 같이 초기값을 설정하면 오차가 최소가 되도록 5개의 파라메터를 추정할 수 있다. 아래 그림은 이전 시간에 사용한 데이터를 이용하여 엑셀의 해찾기 기능으로 파라메터를 추정한 결과이다 (세부 계산 결과는 첨부파일 참조).

추정 절차 요약:
1. 관측된 내재변동성 (IV) 제곱한다.
2. 관측된 IV로 초기값을 계산하고, 5개의 파라메터에 초기값을 넣는다.
3. 5개의 파라메터를 이용하여 SVI를 계산한다.
4. IV를 제곱한 것과 SVI와의 차이를 계산하고 제곱한다 (Square Error : SE).
5. SE의 평균값을 계산해 놓는다 (Mean Square Error : MSE)
6. 엑셀의 해찾기를 이용하여 MSE가 최소가 되도록 5개의 파라메터를 추정한다.

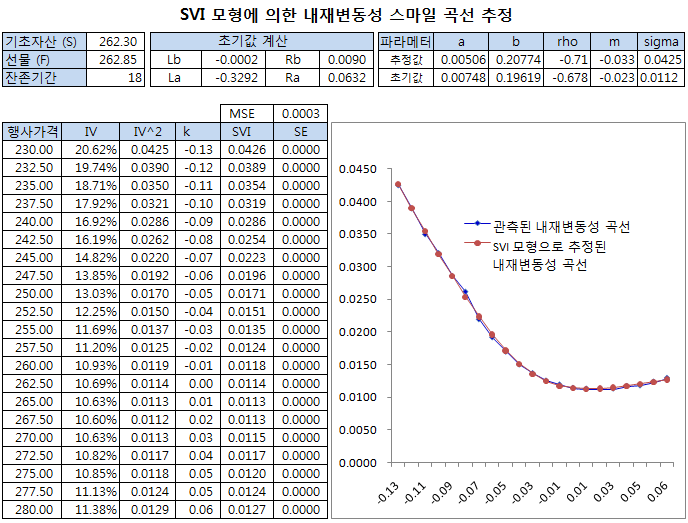
추정된 파라메터로 SVI를 계산한 결과와 IV를 제곱한 결과가 잘 일치한다. 위 그림에서 파란색은 관측된 IV를 제곱한 곡선이고, 빨간색은 추정된 SVI 곡선이다. 두 곡선이 거의 일치하고 있다 (파란색이 잘 안보임).

아래 그림은 SVI에 루트를 씌운 것 (분산이 아닌 표준편차)을 그린 것이다. 이것이 추정된 내재변동성 곡선이다. SVI 함수식을 알고 있으므로, 관측 영역 이외의 영역까지 추정해 볼 수 있다. 우리나라 옵션 시장은 행사가격의 수가 적은 편이므로 넓은 영역의 내재변동성 분포를 알기 위해서는 그림과 같이 외삽법 (Extrapolation)으로 추정해 볼 수 있다. SVI로 추정된 곡선을 시간대별 혹은 일별로 관찰하면 곡선의 형태가 변하는 것을 육안으로 관찰할 수 있고, 5개의 파라메터를 이용하면 곡선이 변하는 정도를 계량화 할 수 있다.

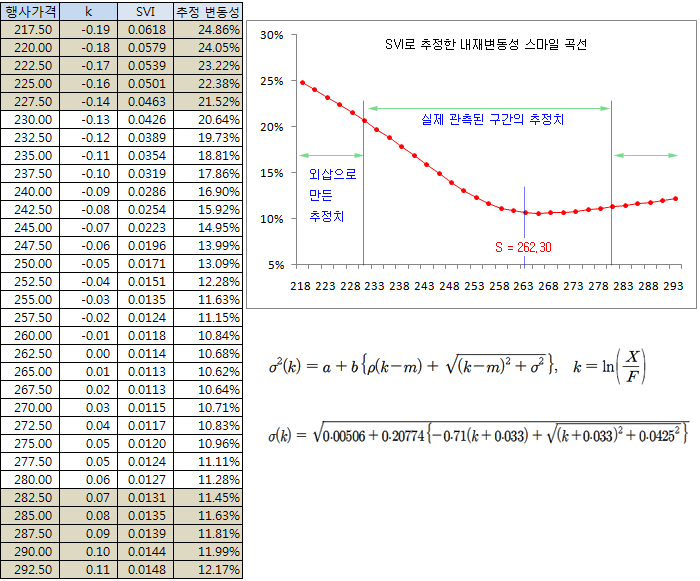
여기까지 내재변동성 스마일 곡선을 추정하는 방법에 대해 알아보았다. 다음 시간에는 이 결과를 이용하여 옵션 만기시 기초자산 수익률 분포 (Risk Neutral Density : RND or State Price Density : SPD)를 추정하는 방법에 대해 살펴보기로 한다.

[출처]36. 내재변동성 곡선 추정식 (SVI)|작성자아마퀀트