News & Events
금융 수학 (12)
금융수학 – 블랙숄즈 옵션공식의 유도(마팅게일)
그 동안 살펴본 기하 브라운 운동 (Geometric Brownian Motion), 위험중립확률 (Risk Neutral Probability), 마팅게일 (Martingale)의 성질을 이용하면 블랙숄즈의 옵션공식을 간단히 유도해 볼 수 있다. 이전에 4편의 포스트를 통해 상당히 복잡한 과정으로 블랙숄즈 옵션공식을 편미분방정식 (PDE)을 이용하여 유도해 보았었다. 이번에는 위험중립확률과 마팅게일 성질을 이용한 방법으로 유도해 보겠다. 상당히 간편한 방법임을 알 수 있다.
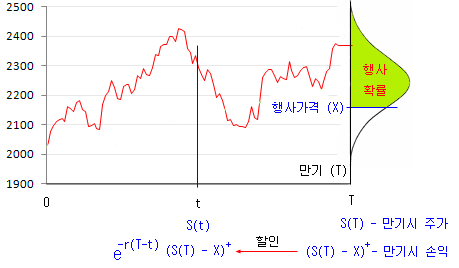
아래 그림은 만기가 (T)이고, 행사가격이 (X)인 옵션의 현재가치 (t 시점에서의 가치)를 표현한 것이다. 이 옵션의 만기 시점(T)의 가치는 [S(T) – X]+ 이고, 이 가치를 이자율 r을 사용하여 t 시점으로 할인하여 옮기면 그림과 같이 된다. 이 값을 이용하면 옵션의 현재가치를 계산할 수 있다. [S(T) – X]+ 의 의미는, 만기 시 옵션의 Pay Off로, 행사 가능한 경우는 S(T) – X > 0 이고, 행사 불가능한 경우는 S(T) – X = 0 임을 의미한다 (Max[S(T) – X, 0] 과 동일한 표현이다).
옵션의 현재가치는 기초자산의 주가 S(T)에 따라 결정되고, S(T)는 마팅게일로 표현되므로, 옵션의 현재가치도 마팅게일로 표현할 수 있다. 식 (1)은 옵션의 현재가치에 대한 마팅게일의 표현이다. t시점의 주가가 St인 상태를 나타낸 것이 Ft 이다. 즉, t-시점의 주가는 St로 알고 있는 상태이므로 (Ft = St), 조건부 기댓값을 사용하여 식 (1)과 같이 마팅게일로 표현할 수 있다.
식 (1)은, t시점의 주가를 알고 있는 상태에서 T-t 기간 이후인 T 시점에서 콜옵션의 기대 가치 (위험중립확률 하에서의)를 무위험 이자율 r로 할인하여 t시점으로 옮긴 가치가 현재의 콜옵션의 가치가 된다는 의미이다.

식 (2)는 t-시점의 기초자산에 대한 기하 브라운 운동의 표현이고, 식 (3)은 현재 시점 (t) 에서부터 만기 시점 (T) 까지 기초자산의 기하 브라운 운동을 표현한 식이다. 여기서 물결무늬는 모두 위험중립확률의 측도 (Measurement)가 사용되었음을 표시한 것이다. 식 (3)을 표준정규분포 확률변수인 Y를 사용하여 나타내면 식 (4)와 같이 쓸 수 있다. 확률변수 Y는 브라운 운동의 특성으로 표준정규분포로 알려져 있다 (여기서는 위험중립확률로 표현된 표준정규분포이다). 변동성인 시그마와 무위험 이자율 r은 상수로 가정하였다.
식 (1)에 식 (4)를 대입하면 아래와 같이 식 (5)를 얻을 수 있다 (St를 간단히 S로 표현하였음). 식 (5)는 확률변수 S 와 또 다른 확률변수 exp(~Y~) 의 곱으로 표시된 식이다. Ft는 t-시점의 St에 관한 정보이지만, exp(~Y~)와는 무관하므로, St와 exp(~Y~)의 곱으로 표현된 새로운 확률변수에 대한 정보로는 가치가 없다. 따라서 조건부 기댓값의 의미가 없어지므로, 식 (6) 처럼 Ft 없이 일반 기댓값으로 표시가 가능하다. 조건부 기댓값 E[A|B]는 B인 조건하에서 A의 기댓값의 의미인데, A와 B가 서로 독립이면 E[A|B] = E[A] 가된다.
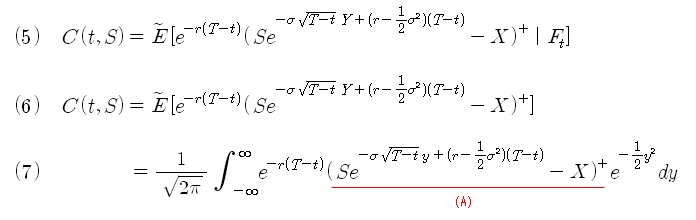
식 (6)을 확률밀도함수로 표시하면 식 (7)과 같이 된다. 또한 (A)가 항상 0 보다 큰 절대부등식을 만족하려면 y는 조건 (9)를 만족하여야 한다. 조건 (9)는 식 (8)의 부등식을 풀어 y의 범위를 구한 것이다.
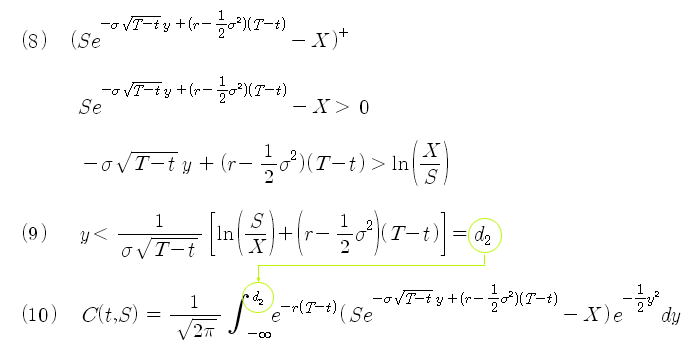
식 (7)에 조건 (9)를 이용하여 적분구간을 조정하면 식 (7)은 식 (10)이 된다. y는 항상 d2 보다 작아야 하므로 적분구간을 d2 까지로 조정하면 식 (7)의 (A) 부분에서 (+) 기호를 없앨 수 있다. 이제 식 (10)을 식 (11)과 같이 정리하여 누적확률분포로 나타내면 최종적으로 식 (13)을 얻을 수 있고, 이 식이 바로 블랙숄즈의 옵션공식이 된다.