News & Events
[금융수학] 10. 금융수학 – 위험중립확률 (Risk Neutral Probability)
금융 수학 (10)
금융수학 – 위험중립확률 (Risk Neutral Probability)
위험중립확률은 게임이 공정하게 되기 위한 조건의 확률을 말한다. 위험중립확률은 재무관리 (Financial Management)에서는 옵션 가격결정 모형 중 이항 모형 (C-R 모형)에서 주로 사용되며, 금융공학 (Financial Engineering)에서는 마팅게일 (Martingale)이라는 성질과 더불어 대단히 중요한 개념으로 사용된다.
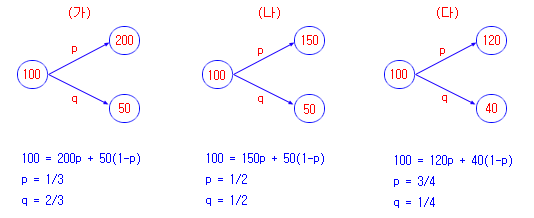
위험중립확률에 대해 간단히 개념을 잡기위해 아래와 같은 3가지 게임을 생각해 보자. 그림 (가)는 100원을 투자했을 때 이기면 원금의 2배인 200원이 되고, 지면 원금의 1/2배인 50원이 되는 경우이다. (나)와 (다)도 그림과 같이 되고, 이길 확률과 질 확률은 모두 50% 씩이라고 가정하자.
단순히 생각하여 게임 (가)의 기댓값은 125원 (=200*0.5 + 50*0.5)이 되고, (나)와 (다)는 각각 100원과 80원이 된다. 그러면 참가자 입장에서는 게임 (가)가 가장 유리한 게임이 되고, (나)는 공정한 게임, 그리고 (다)는 불리한 게임이 될 것이다.
이 3게임을 모두 공정한 게임으로 만들려면, 즉 기댓값이 모두 100원이 나오게 하려면, 이길 확률과, 질 확률을 50% 씩이 아닌 다른 확률로 만들어야 한다. 각 그림 아래에 기댓값이 모두 100원이 나오도록 확률을 조정해 보았더니, 그림 (가)는 이길 확률이 1/3 (33.3%)이고, 질 확률이 2/3 (66.6%)이 나왔다. 이길 확률이 50% 보다 작아져야 공정한 게임이 된다는 것을 의미한다. (나)의 경우는 원래 공정한 게임이었으므로, 확률에 변화가 없다. (다)는 (가)와 반대의 경우로 이길 확률이 높아져야 한다.
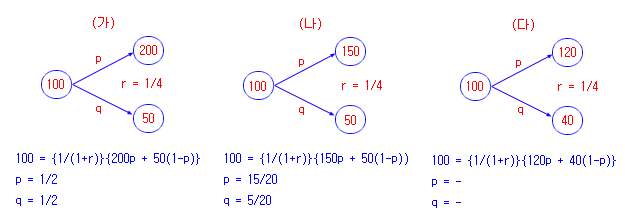
이번에는 위의 경우에 이자율 (r)이 존재하는 경우를 생각해 보자. 아래의 게임 (가)는 이자율 (r)이 1/4 (25%) 이며, 원금 100원을 은행에 넣어두면 1기간 후에는 125원이 되는 상황이다. 만약 승률이 50%인 이 게임에 참가했다면 1기간 후의 기댓값은 125원이 되므로 은행에 넣어둔 것과 동일한 결과가 된다. 즉, 이 게임은 공정한 게임이 된다. 반면에 (나)와 (다)는 승률이 50%라면 기댓값이 125원 이하이므로 참가자에게 불리한 게임이 된다.
이 경우도 모두 공정한 게임이 되도록 확률을 조정해 주면 아래 그림의 p, q와 같이 된다. 계산 방법은 이길 확률을 p, 질 확률을 (1-p)로 놓고, 1기간 후의 기댓값을 구한 다음, (r) 로 할인하여 현재 가치를 구한 값이 원금인 100원과 같아지면 된다. 게임 (다)의 경우는 1기간 후의 값들이 모두 125원 보다 작은 값이므로 아무도 이 게임에 참여하지 않을 것이다. 따라서 p, q도 계산되지 않는다 (p,q 모두 1보다 작아야 하고, p+q=1 이어야 함).
위의 경우처럼 게임이 공정해 지도록 조정한 확률을 위험중립확률이라고 한다. 위험중립확률을 이용하면, 확률이 이자율을 이미 포함하고 있으므로 이자율을 따로 고려해 주지 않아도 되기 때문에 계산이 편리해진다.
위험중립확률을 일반적으로 표현하면 아래와 같다. 원금 S가 1기간 후에, u배 상승한 경우는 u*S가 되고, d배 하락한 경우는 d*S 가 된다. 또한, 원금 S는 1기간 후에 이자율 (r)이 적용되어, (1+r)*S 가 된다. 위험중립확률로 1기간 후의 기댓값을 구해서, 1기간 이전의 가치로 환산하면 원금인 S와 같아져야 한다. 이때의 확률이 위험중립확률이 되고, p, q 위에 물결무늬를 붙여서 표기한다. 단, 위의 그림에서 (다)와 같은 상황이 발생하지 않으려면, (0 < d < 1+r < u)의 관계가 성립하여야 한다.
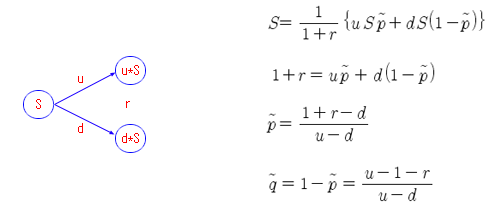
2 기간 모형인 경우도 아래와 같이 동일한 결과가 나온다. 그림과 같이 위험중립확률을 적용하여 2기간 후의 기댓값을 구한 다음, 이자율 r 을 사용하여 2기간 앞으로 복리로 할인하여, 원금과 같아지는 확률을 계산하면 된다.
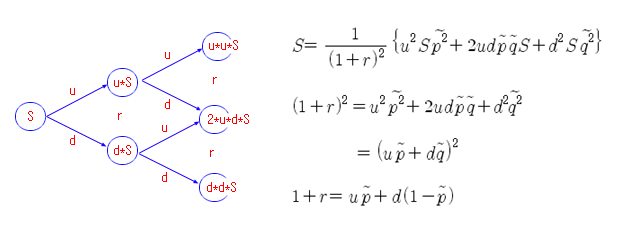
위험중립확률을 이용한 통계값은 아래와 같이 모두 물결무늬를 붙여서 표기한다.
참고로 몬테카를로 시뮬레이션으로 100일 후의 코스피 지수를 예측해 본 결과, 3월 23일 현재의 코스피 지수가 2,026.83 이고, 100 거래일 후에는 1,780 ~ 2,406이 나왔었다 (내재 변동성 사용 시). 연간 무위험 이자율을 5%라고 하면, 100 거래일 동안의 이자율은 약 2% 정도가 된다. 그러면 원금이 2,026.83 이고, 100일 후 상승하면 2,406이 되고, 하락하면 1,780이 된다고 할 때, 위험중립확률은 아래와 같이 된다. 상승 확률이 46% 만 되어도 공정한 게임이 된다고 할 수 있으므로, 예측대로만 된다면 투자자에게 유리한 게임이 된다. 사실 이 결과는 몬테카를로 시뮬레이션 당시 연간 주가의 성장률을 이미 10%로 적용하여 예측치가 높게 나왔기 때문에 상승 위험중립확률이 작게 나온 것이다.
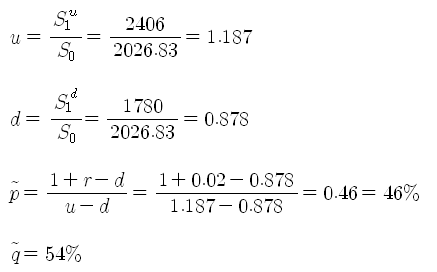
위험중립확률은 마팅게일이라는 개념과 함께 금융공학에서 대단히 중요한 개념으로 사용된다. 어떤 게임이 공정한 게임이 된다는 것은, 공정한 가격을 산출할 수 있다는 의미가 되고, 재무관리나 금융공학의 주요 이슈인 금융상품의 적정가격을 산출할 수 있다는 의미가 된다. 다음 포스트에서는 마팅게일 (Martingale)의 성질에 대해 살펴보도록 하겠다.
